
【题目】已知函数 ![]() (a<0). (Ⅰ)当a=﹣3时,求f(x)的单调递减区间;
(a<0). (Ⅰ)当a=﹣3时,求f(x)的单调递减区间;
(Ⅱ)若函数f(x)有且仅有一个零点,求实数a的取值范围.
【答案】解:(Ⅰ)∵a=﹣3,∴ ![]() ,
,
故 ![]() ,
,
令f′(x)<0,解得﹣3<x<﹣2或x>0,
即所求的单调递减区间为(﹣3,﹣2)和(0,+∞);
(Ⅱ)∵ ![]() (x>a),
(x>a),
令f′(x)=0,得x=0或x=a+1,
当a+1>0,即﹣1<a<0时,
f(x)在(a,0)和(a+1,+∞)上为减函数,在(0,a+1)上为增函数,
由于f(0)=aln(﹣a)>0,当x→a时,f(x)→+∞,
当x→+∞时,f(x)→﹣∞,于是可得函数f(x)图象的草图如图:
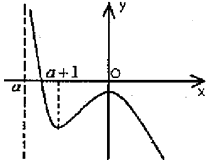
此时函数f(x)有且仅有一个零点.
即当﹣1<a<0对,f(x)有且仅有一个零点;
当a=﹣1时, ![]() ,
,
∵ ![]() ,∴f(x)在(a,+∞)单调递减,
,∴f(x)在(a,+∞)单调递减,
又当x→﹣1时,f(x)→+∞.当x→+∞时,f(x)→﹣∞,
故函数f(x)有且仅有一个零点;
当a+1<0即a<﹣1时,
f(x)在(a,a+1)和(0,+∞)上为减函数,在(a+1,0)上为增函数,
又f(0)=aln(﹣a)<0,当x→a时,f(x)→+∞,当x→+∞时,f(x)→﹣∞,
于是可得函数f(x)图象的草图如图:
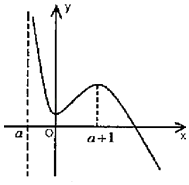
此时函数f(x)有且仅有一个零点;
综上所述,所求的范围是a<0.
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的递减区间即可;(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间,结合函数的图象求出a的具体范围即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点. 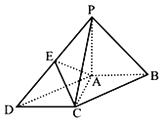
(1)求证:AC⊥PB;
(2)当二面角E﹣AC﹣D的大小为45°时,求AP的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,圆柱的高为2,底面半径为![]() ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过![]() 作圆柱的截面交下底面于
作圆柱的截面交下底面于![]() ,四边形ABCD是正方形.
,四边形ABCD是正方形.
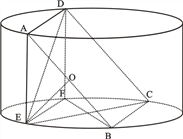
(1)求证![]() ;
;
(2)求四棱锥E-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D为线段AC的中点.

(1)求证:PA⊥BD.
(2)求证:BD⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三人独立破译同一份密码.已知三人各自破译出密码的概率分别为 ![]() ,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型: ![]() ,其中x表示经过的时间,
,其中x表示经过的时间, ![]() 表示x=0时的人口,r表示人口的平均增长率.
表示x=0时的人口,r表示人口的平均增长率.
下表是1950―1959年我国人口数据资料:

如果以各年人口增长率的平均值作为我国这一时期的人口增长率,用马尔萨斯人口增长模型建立我国这一时期的具体人口增长模型,某同学利用图形计算器进行了如下探究:
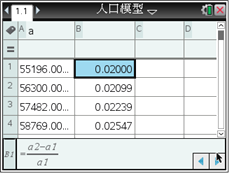
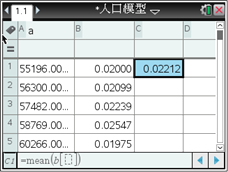
由此可得到我国1950―1959年我国这一时期的具体人口增长模型为____________. (精确到0.001)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x)的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com