
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=![]() .
.

(Ⅰ)证明:平面A1BD∥平面CD1B1;
(Ⅱ)求三棱柱ABD﹣A1B1D1的体积.
【答案】(Ⅰ)详见解析(Ⅱ)1
【解析】试题分析:(1)要证明![]() ⊥平面
⊥平面![]() ,只要证明
,只要证明![]() 垂直于平面
垂直于平面![]() 内的两条相交直线即可,由已知可证出
内的两条相交直线即可,由已知可证出![]() ⊥BD,取
⊥BD,取![]() 的中点为
的中点为![]() ,通过证明四边形
,通过证明四边形![]() 为正方形可证
为正方形可证![]() ⊥
⊥![]() .由线面垂直的判定定理问题得证;(2)由已知
.由线面垂直的判定定理问题得证;(2)由已知![]() 是三棱柱ABD﹣A1B1D1的高,由此能求出三棱柱ABD﹣A1B1D1的体积
是三棱柱ABD﹣A1B1D1的高,由此能求出三棱柱ABD﹣A1B1D1的体积
试题解析:(Ⅰ)∵四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=![]() ,由棱柱的性质可得BB1和DD1平行且相等,故四边形BB1D1D为平行四边形,故有BD和B1D1平行且相等.而BD不在平面CB1D1内,而B1D1在平面CB1D1内,∴BD∥平面CB1D1.同理可证,A1BCD1为平行四边形,A1B∥平面CB1D1.而BD和A1B是平面A1BD内的两条相交直线,故有平面A1BD∥平面CD1B1 .
,由棱柱的性质可得BB1和DD1平行且相等,故四边形BB1D1D为平行四边形,故有BD和B1D1平行且相等.而BD不在平面CB1D1内,而B1D1在平面CB1D1内,∴BD∥平面CB1D1.同理可证,A1BCD1为平行四边形,A1B∥平面CB1D1.而BD和A1B是平面A1BD内的两条相交直线,故有平面A1BD∥平面CD1B1 .
(Ⅱ)由题意可得A1O为三棱柱ABD﹣A1B1D1的高.三角形A1AO中,由勾股定理可得A1O=![]() =
=![]() =1,
=1,
∴三棱柱ABD﹣A1B1D1的体积V=S△ABDA1O=![]() A1O=
A1O=![]() ×1=1.
×1=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c,其中b,c∈R.
(1)当f(x)的图象关于直线x=1对称时,b=______;
(2)如果f(x)在区间[-1,1]不是单调函数,证明:对任意x∈R,都有f(x)>c-1;
(3)如果f(x)在区间(0,1)上有两个不同的零点.求c2+(1+b)c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )

A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2ax+5.
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若a≤1,求函数y=|f(x)|在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品近一个月内(30天)预计日销量![]() (件)与时间t(天)的关系如图1所示,单价
(件)与时间t(天)的关系如图1所示,单价![]() (万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
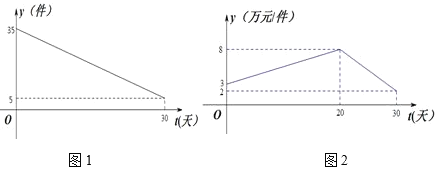
(1)试写出![]() 与
与![]() 的解析式;
的解析式;
(2)求此商品日销售额的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点
,B为AC的中点,分别以AB,AC为直径在AC的同侧作半圆,M,N分别为两半圆上的动点![]() 不含端点A,B,
不含端点A,B,![]() ,且
,且![]() ,则
,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=![]() ,设bn=
,设bn=![]() ,n∈N*。
,n∈N*。
(1)证明{bn}是等比数列(指出首项和公比);
(2)求数列{log2bn}的前n项和Tn。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,茎叶图记录了甲、乙两组各4名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中以X表示。

(1)如果x=8,求乙组同学植树棵数的平均数和方差;
(2)如果x=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com