
分析 (I)推导出$f'(x)=\frac{a}{ax+b}+2x$,利用导数的几何意义列出方程组,能求出a,b的值.
(II)设g(x)=f(x)-(x2+x),则g(x)=ln(ax+b)-x,依题意g(x)≤0恒成立,根a<0,a>0两种情况分类讨论,利用导数性质能求出ab的最大值.
解答 解:(I)∵f(x)=ln(ax+b)+x2(a≠0),
∴$f'(x)=\frac{a}{ax+b}+2x$,
∵曲线y=f(x)在点(1,f(1))处的切线方程为y=x,
∴$\left\{\begin{array}{l}f'(1)=\frac{a}{a+b}+2=1\\ f(1)=ln({a+b})+1=1\end{array}\right.$,
解得,a=-1,b=2;
(II)设g(x)=f(x)-(x2+x),则g(x)=ln(ax+b)-x,依题意g(x)≤0恒成立,
①a<0时,g(x)定义域$({-∞,-\frac{a}{b}})$,
取x0使得$ln({a{x_0}+b})=-\frac{a}{b}+1$,得${x_0}=\frac{{{e^{-\frac{b}{a}}}-b}}{a}<-\frac{b}{a}$,
则$g({x_0})=ln({a{x_0}+b})-{x_0}>ln({a{x_0}+b})-({-\frac{b}{a}})=({-\frac{b}{a}+1})+\frac{b}{a}=1>0$
与g(x)≤0矛盾,∴a<0不符合要求,
②a>0时,$g'(x)=\frac{a}{ax+b}-1=\frac{{-a({x-\frac{a-b}{a}})}}{ax+b}({ax+b>0})$,
当$-\frac{b}{a}<x<\frac{a-b}{a}$时,g'(x)>0;当$x>\frac{a-b}{a}$时,g'(x)<0,
∴g(x)在区间$({-\frac{b}{a},\frac{a-b}{a}})$上为增函数,在区间$({\frac{a-b}{a},+∞})$上为减函数,
∴g(x)在其定义域$({-\frac{b}{a},+∞})$上有最大值,最大值为$g({\frac{a-b}{a}})$,
由g(x)≤0,得$g({\frac{a-b}{a}})=lna-\frac{a-b}{a}≤0$,∴b≤a-alna,∴ab≤a2-a2lna,
设h(a)=a2-a2lna,则h'(a)=2a-(2alna+a)=a(1-2lna),
∴$0<a<\sqrt{e}$时,$h'(a)>0;a>\sqrt{e}$时,h'(a)<0,
∴h(a)在区间$({0,\sqrt{e}})$上为增函数,在区间$({\sqrt{e},+∞})$上为减函数,
∴h(a)的最大值为$h({\sqrt{e}})=e-\frac{e}{2}=\frac{e}{2}$,
∴当$a=\sqrt{e},b=\frac{{\sqrt{e}}}{2}$时,ab取最大值为$\frac{e}{2}$,
综合①,②得,ab最大值为$\frac{e}{2}$.
点评 本题考查实数值的求法,考查两数积最大值的求法,考查导数性质、导数的几何意义、构造法、函数单调性等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想,是中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )| A. | [-1,2] | B. | [-1,0)∪(1,2] | C. | [0,1] | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{22}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 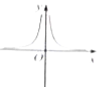 | B. | 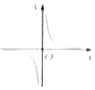 | C. | 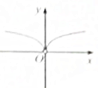 | D. | 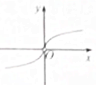 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{{\sqrt{3}}}{3}}]$ | B. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | C. | $[{-\frac{1}{2},\frac{1}{2}}]$ | D. | $[{0,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,+∞) | B. | ($\frac{3}{4}$,+∞) | C. | (2,+∞) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com