
| A. | ($\frac{5}{2}$,+∞) | B. | ($\frac{3}{4}$,+∞) | C. | (2,+∞) | D. | ($\frac{3}{2}$,+∞) |
分析 由诱导公式化简f(x),判断f(x)是奇函数,再由题意和函数的周期公式列出不等式,求出ω的取值范围.
解答 解:函数f(x)=2cos(ωx+$\frac{3π}{2}$)=2sinωx(ω>0),
所以f(x)=2sinωx是奇函数,
又存在m∈[$-\frac{2π}{3}$,0),n∈(0,$\frac{π}{4}$],使得f(m)-f(n)=0,
所以函数f(x)的周期T=$\frac{2π}{ω}$<2×$\frac{2π}{3}$,解得ω>$\frac{3}{2}$,
则ω的取值范围是($\frac{3}{2}$,+∞).
故选:D.
点评 本题考查了诱导公式以及三角函数的周期性和奇偶性的应用问题,是基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:选择题
为了得到函数 的图像,只需将
的图像,只需将 的图像上每一点
的图像上每一点
A.向左平移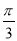 个单位长度
个单位长度
B.向右平移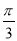 个单位长度
个单位长度
C.向左平移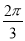 个单位长度
个单位长度
D.向右平移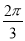 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com