
| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
分析 延长AG交BC于D,得出点G、E是AD的三等分点,D是BC的中点;用$\overrightarrow{DG}$、$\overrightarrow{BD}$表示出$\overrightarrow{BA}$、$\overrightarrow{CA}$,$\overrightarrow{BG}$和$\overrightarrow{CG}$,根据数量积的定义列出方程组求出${\overrightarrow{DG}}^{2}$和${\overrightarrow{BD}}^{2}$的值,再计算$\overrightarrow{BE}$•$\overrightarrow{CE}$的值.
解答 解:延长AG交BC于D,如图所示,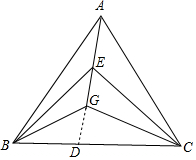
G是△ABC的重心,点E是AG的中点,
∴$\overrightarrow{DG}$=$\overrightarrow{GE}$=$\overrightarrow{EA}$=$\frac{1}{3}$$\overrightarrow{DA}$,$\overrightarrow{BD}$=$\overrightarrow{CD}$;
∴$\overrightarrow{BA}$=$\overrightarrow{BD}$+$\overrightarrow{DA}$=$\overrightarrow{BD}$+3$\overrightarrow{DG}$,
$\overrightarrow{CA}$=$\overrightarrow{CD}$+$\overrightarrow{DA}$=-$\overrightarrow{BD}$+3$\overrightarrow{DG}$,
∴$\overrightarrow{BA}$•$\overrightarrow{CA}$=($\overrightarrow{BD}$+3$\overrightarrow{DG}$)•(-$\overrightarrow{BD}$+3$\overrightarrow{DG}$)=9${\overrightarrow{DG}}^{2}$-${\overrightarrow{BD}}^{2}$=4①,
又$\overrightarrow{BG}$=$\overrightarrow{BD}$+$\overrightarrow{DG}$,
$\overrightarrow{CG}$=$\overrightarrow{CD}$+$\overrightarrow{DG}$=-$\overrightarrow{BD}$+$\overrightarrow{DG}$,
∴$\overrightarrow{BG}$•$\overrightarrow{CG}$=($\overrightarrow{BD}$+$\overrightarrow{DG}$)•(-$\overrightarrow{BD}$+$\overrightarrow{DG}$)=${\overrightarrow{DG}}^{2}$-${\overrightarrow{BD}}^{2}$=-1②,
由①②组成方程组,解得${\overrightarrow{DG}}^{2}$=$\frac{5}{8}$,${\overrightarrow{BD}}^{2}$=$\frac{13}{8}$;
∴$\overrightarrow{BE}$•$\overrightarrow{CE}$=($\overrightarrow{BD}$+$\overrightarrow{DE}$)•($\overrightarrow{CD}$+$\overrightarrow{DE}$)
=($\overrightarrow{BD}$+2$\overrightarrow{DG}$)•(-$\overrightarrow{BD}$+2$\overrightarrow{DG}$)
=4${\overrightarrow{DG}}^{2}$-${\overrightarrow{BD}}^{2}$
=4×$\frac{5}{8}$-$\frac{13}{8}$=$\frac{7}{8}$.
故选:C.
点评 本题考查了平面向量的数量积运算和线性运算问题,也考查了数形结合的应用思想,是中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一项限角或第二象限角 | B. | 第二象限角或第四象限角 | ||
| C. | 第一象限角或第三象限角 | D. | 第二象限角或第三象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3\sqrt{7}}{7}$ | B. | $\frac{3\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{3}$ | D. | -$\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )| A. | [-1,2] | B. | [-1,0)∪(1,2] | C. | [0,1] | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,+∞) | B. | ($\frac{3}{4}$,+∞) | C. | (2,+∞) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com