
分析 根据题意,由双曲线的方程计算可得其渐近线方程为y=±$\frac{x}{a}$,进而由直线垂直的性质分析可得有$\frac{1}{a}$=$\frac{1}{2}$,解可得a的值,由双曲线的几何性质可得c的值,进而有双曲线的离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-y2=1,则其渐近线方程为y=±$\frac{x}{a}$,
又由双曲线的一条渐近线与直线2x+y-3=0即y=-2x+3垂直,
则有$\frac{1}{a}$=$\frac{1}{2}$,
即a=2,
又由b=1,则c=$\sqrt{4+1}$=$\sqrt{5}$,
则双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$;
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查双曲线的几何性质,关键掌握双曲线的渐近线方程.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
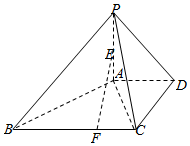 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|2≤x≤4} | D. | {x|2<x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
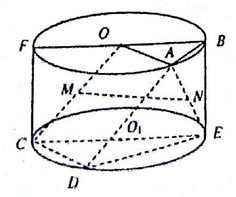 如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.
如图,矩形FCEB是圆柱OO1的轴截面,且FC=1,FB=2,点A、D分别在上下底面圆周上,且在面FCEB的同侧,△OAB是等边三角形,∠ECD=60°,M、N分别是OC、AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com