
分析 设直线l的方程,代入抛物线的方程,由韦达定理及抛物线的焦点弦公式求得丨AB丨,利用中点坐标公式,求得中点M坐标,利用点斜式方程,求得直线AB垂直平分线方程,当y=0,求得P点坐标,求得丨PF丨,即可求得|$\frac{AB}{PF}$|.
解答 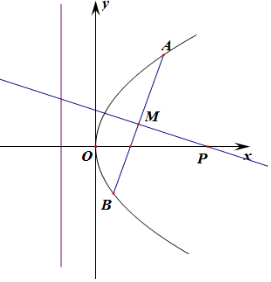 解:设直线AB的方程y=k(x-2),(k≠0),A(x1,y1),B(x2,y2),
解:设直线AB的方程y=k(x-2),(k≠0),A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{y=k(x-2)}\\{{y}^{2}=8x}\end{array}\right.$,k2x2-(4k2+8)+4k2=0,
x1+x2=$\frac{4{k}^{2}+8}{{k}^{2}}$,x1x2=4,
丨AB丨=x1+x2+p=$\frac{8{k}^{2}+8}{{k}^{2}}$,
则y1+y2=$\frac{8}{k}$,
则AB的中点M($\frac{2{k}^{2}+4}{{k}^{2}}$,$\frac{4}{k}$),
直线AB垂直平分线方程:y-$\frac{4}{k}$=-$\frac{1}{k}$(x-$\frac{2{k}^{2}+4}{{k}^{2}}$),
当y=0,解得:x=$\frac{6{k}^{2}+4}{{k}^{2}}$,
丨PF丨=$\frac{6{k}^{2}+4}{{k}^{2}}$-2=$\frac{4{k}^{2}+4}{{k}^{2}}$,
∴|$\frac{AB}{PF}$|=$\frac{\frac{8{k}^{2}+8}{{k}^{2}}}{\frac{4{k}^{2}+4}{{k}^{2}}}$=2,
∴|$\frac{AB}{PF}$|=2,
故答案为:2.
点评 本题考查直线与抛物线的位置关系,考查中点坐标公式,韦达定理,抛物线的焦点弦公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
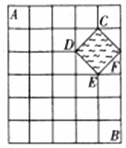 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
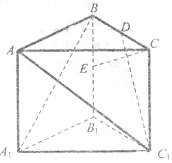 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com