
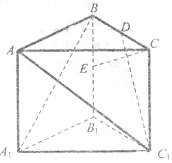
 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.分析 (1),连接A1C交AC1于点F,可得DF为△A1BC的中位线,即DF∥A1B,可证A1B∥面AC1D
(2易得AD⊥面B1BCC1,AD⊥CE,
由D,E分别是BC,BB1的中点,可得CE⊥DC,即可证CE⊥面AC1D
(3)如图由(2)得CE⊥面AC1D,则∠HFC就是二面角C-AC1-D的平面角,
在Rt△CHF中,sin∠HFC=$\frac{CH}{CF}=\frac{2}{\sqrt{5}}×\frac{1}{\sqrt{2}}=\frac{\sqrt{10}}{5}$
解答 解:(1)如图,连接A1C交AC1于点F,则F为AC1的中点,
∴DF为△A1BC的中位线,故DF∥A1B,
A1B?面AC1D,DF?面AC1D,
∴A1B∥面AC1D;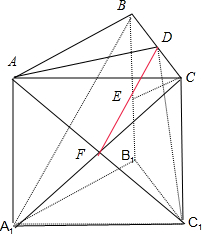
(2)∵正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点,
∴AD⊥面B1BCC1,∴AD⊥CE,
在正方形B1BCC1中,∵D,E分别是BC,BB1的中点,可得△ECB≌DC1C,
∴∠ECB=∠DC1C,
即∠CDC1+∠ECB=90°.∴CE⊥DC,
且AD∩CD=D,∴CE⊥面AC1D;
(3)如图由(2)得CE⊥面AC1D,设CE交DC1于H,连接HF,
则∠HFC就是二面角C-AC1-D的平面角,
在正方形BB1C1C中,由射影定理得CC12=C1D•C1H,⇒${C}_{1}H=\frac{4}{\sqrt{5}}$
由$C{H}^{2}+{C}_{1}{H}^{2}=C{{C}_{1}}^{2}$,⇒CH=$\frac{2}{\sqrt{5}}$.
在Rt△CHF中,sin∠HFC=$\frac{CH}{CF}=\frac{2}{\sqrt{5}}×\frac{1}{\sqrt{2}}=\frac{\sqrt{10}}{5}$.
∴二面角C-AC1-D的正弦值为$\frac{\sqrt{10}}{5}$.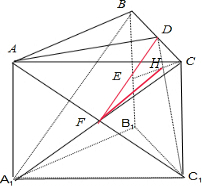
点评 本题考查了空间线线、线面的位置关系,考查了转化思想,空间想象能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
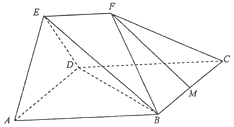 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:解答题
执行如下程序框图:
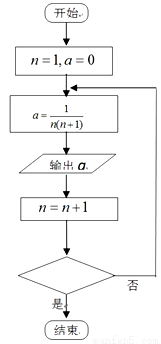
(1)如果在判断框内填入“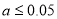 ”,请写出输出的所有数值;
”,请写出输出的所有数值;
(2)如果在判断框内填入“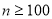 ”,试求出所有输出数字的和。
”,试求出所有输出数字的和。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com