
分析 (Ⅰ)设“该选手连续答对3道题晋级”的事件为A,
利用相互独立事件的概率公式求概率即可;
(Ⅱ)该选手在竞赛中答对题的个数为X,写出X的可能取值,
计算对应的概率值,写出X的分布列,求出数学期望值.
解答 解:(Ⅰ)设“该选手连续答对3道题晋级”的事件为A,
则P(A)=${(\frac{2}{3})}^{3}$+$\frac{1}{3}$×${(\frac{2}{3})}^{3}$+${(\frac{1}{3})}^{2}$×${(\frac{2}{3})}^{3}$=$\frac{104}{243}$;
(Ⅱ)该选手在竞赛中答对题的个数为X,则X的可能取值为0,1,2,3;
P(X=0)=${(\frac{1}{3})}^{5}$=$\frac{1}{243}$;
P(X=1)=${C}_{5}^{1}$×$\frac{2}{3}$×${(\frac{1}{3})}^{4}$=$\frac{10}{243}$;
P(X=2)=${C}_{5}^{2}$×${(\frac{2}{3})}^{2}$×${(\frac{1}{3})}^{3}$=$\frac{40}{243}$;
P(X=3)=${(\frac{2}{3})}^{3}$+${C}_{3}^{1}$×$\frac{1}{3}$×${(\frac{2}{3})}^{3}$+${C}_{4}^{2}$×${(\frac{1}{3})}^{2}$${×(\frac{2}{3})}^{3}$=$\frac{64}{81}$
(或P(X=3)=1-$\sum_{i=1}^{3}$P(X=i-1)=1-($\frac{1}{243}$+$\frac{10}{243}$+$\frac{40}{243}$)=$\frac{64}{81}$);
∴随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| p | $\frac{1}{243}$ | $\frac{10}{243}$ | $\frac{40}{243}$ | $\frac{64}{81}$ |
点评 本题考查了相互独立事件的概率以及离散型随机事件的分布列和数学期望值的计算问题,是中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
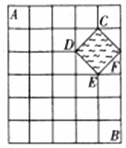 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
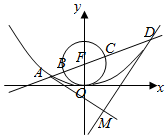 已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.
已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
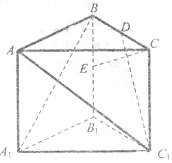 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某程序的框图如图所示,执行该程序,若输入的N=5,则输出i=( )
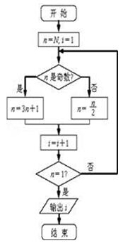
A.9 B.8 C.7 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com