
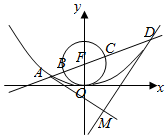
 已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.
已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.分析 (1)求得P和Q点坐标,求得丨QF丨,由题意可知,$\frac{8}{p}$+$\frac{p}{2}$=$\frac{5}{4}$×$\frac{8}{p}$即可求得p的值,求得椭圆方程;
(2)设直线方程,代入抛物线方程,由韦达定理x1x2=-4,求导,根据导数的几何意义,求得切线方程,联立求得M点坐标,根据点到直线距离公式,求得M到l的距离,利用三角形的面积公式,即可求得△ABM与△CDM的面积之积的最小值.
解答 解:(1)由题意可知P(4,0),Q(4,$\frac{8}{p}$),丨QF丨=$\frac{8}{p}$+$\frac{p}{2}$,
由$|{QF}|=\frac{5}{4}|{PQ}|$,则$\frac{8}{p}$+$\frac{p}{2}$=$\frac{5}{4}$×$\frac{8}{p}$,解得:p=2,
∴抛物线x2=4y;
(2)设l:y=kx+1,A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$,整理得:x2-4kx-4=0,
则x1x2=-4,
由y=$\frac{1}{4}$x2,求导y′=$\frac{x}{2}$,
直线MA:y-$\frac{{x}_{1}^{2}}{4}$=$\frac{{x}_{1}}{2}$(x-x1),即y=$\frac{{x}_{1}}{2}$x-$\frac{{x}_{1}^{2}}{4}$,
同理求得MD:y=$\frac{{x}_{2}}{2}$x-$\frac{{x}_{2}^{2}}{4}$,
$\left\{\begin{array}{l}{y=\frac{{x}_{1}x}{2}-\frac{{x}_{1}^{2}}{4}}\\{y=\frac{{x}_{2}x}{2}-\frac{{x}_{2}^{2}}{4}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2k}\\{y=-1}\end{array}\right.$,则M(2k,-1),
∴M到l的距离d=$\frac{2{k}^{2}+2}{\sqrt{1+{k}^{2}}}$=2$\sqrt{1+{k}^{2}}$,
∴△ABM与△CDM的面积之积S△ABM•S△CDM=$\frac{1}{4}$丨AB丨丨CD丨•d2,
=$\frac{1}{4}$(丨AF丨-1)(丨DF丨-1)•d2,
=$\frac{1}{4}$y1y2d2=$\frac{1}{4}$•$\frac{{x}_{1}^{2}{x}_{2}^{2}}{16}$×d2,
=1+k2≥1,
当且仅当k=0时取等号,
当k=0时,△ABM与△CDM的面积之积的最小值1.
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,考查韦达定理,导数的几何意义,点到直线的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|2≤x≤4} | D. | {x|2<x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:填空题
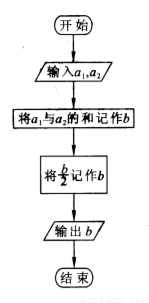
图中所示的是一个算法的流程图,已知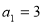 ,输出的
,输出的 ,则
,则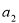 的值是___________.
的值是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com