
分析 (1)求出函数的导数,可得切线的斜率和切点,由点斜式方程可得切线的方程;
(2)求出导数,并分解因式,讨论当a=0,a>0,-$\frac{3}{2}$<a<0时,由导数大于0,可得增区间;导数小于0,可得减区间;
(3)对任意a∈[1,2]及x∈[1,3]时,恒有f(x)≥ta2恒成立等价于f(x)min≥ta2,由(2)可得f(x)的单调性,可得最小值,再由参数分离,可得t≤$\frac{3}{{a}^{2}}$+$\frac{1}{2a}$,a∈[1,2]时恒成立,令g(a)=$\frac{3}{{a}^{2}}$+$\frac{1}{2a}$,求出导数,判断单调性,求得最小值,即可得到所求范围.
解答 解:(1)f(x)=$\frac{1}{2}$x2+3x-4lnx的导数为f′(x)=x+3-$\frac{4}{x}$,
可得曲线y=f(x)在x=1处的切线斜率为1+3-4=0,切点为(1,$\frac{7}{2}$),
故曲线y=f(x)在x=1处的切线方程为y-$\frac{7}{2}$=0(x-1),
即有y=$\frac{7}{2}$;
(2)f(x)=$\frac{1}{2}$ax2+3x-(a+3)lnx(a>-$\frac{3}{2}$)的导数为:
f′(x)=ax+3-$\frac{a+3}{x}$=$\frac{(x-1)(ax+a+3)}{x}$,
当a=0时,f′(x)=$\frac{3(x-1)}{x}$,当0<x<1时,f′(x)<0,f(x)递减;
当x>1时,f′(x)>0,f(x)递增.
当a>0时,-$\frac{a+3}{a}$<1,可得当0<x<1时,f′(x)<0,f(x)递减;
当x>1时,f′(x)>0,f(x)递增.
当-$\frac{3}{2}$<a<0时,-$\frac{a+3}{a}$>1,可得当0<x<1或x>-$\frac{a+3}{a}$时,f′(x)<0,f(x)递减;
当1<x<-$\frac{a+3}{a}$,时,f′(x)>0,f(x)递增.
综上可得,当a≥0时,f(x)在(0,1)递减,在(1,+∞)递增;
当-$\frac{3}{2}$<a<0时,f(x)在(0,1),(-$\frac{a+3}{a}$,+∞)递减;在(1,-$\frac{a+3}{a}$)递增.
(3)由题意可知,对任意a∈[1,2]及x∈[1,3]时,恒有f(x)≥ta2恒成立等价于
f(x)min≥ta2,
由(2)可得当a≥0时,f(x)在x∈[1,3]上递增,f(x)的最小值为f(1)=$\frac{1}{2}$a+3,
任意a∈[1,2]时,$\frac{1}{2}$a+3≥ta2恒成立,
∴t≤$\frac{3}{{a}^{2}}$+$\frac{1}{2a}$,a∈[1,2]时恒成立,
令g(a)=$\frac{3}{{a}^{2}}$+$\frac{1}{2a}$,由g′(a)=-$\frac{6}{{a}^{3}}$-$\frac{1}{2}$•$\frac{1}{{a}^{2}}$<0,
可得g(a)在[1,2]递减,即有g(a)的最小值为g(2)=1,
则实数t的取值范围为t≤1.
点评 本题考查利用导数研究切线方程、函数的单调性及最值及恒成立问题,考查学生综合运用所学知识分析问题解决问题的能力,综合性强.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )| A. | [-1,2] | B. | [-1,0)∪(1,2] | C. | [0,1] | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{{\sqrt{3}}}{3}}]$ | B. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | C. | $[{-\frac{1}{2},\frac{1}{2}}]$ | D. | $[{0,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,+∞) | B. | ($\frac{3}{4}$,+∞) | C. | (2,+∞) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{5π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:填空题
函数y=a1-x(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny-1=0(mn>0)上,则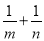 的最小值为________
的最小值为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com