
【题目】已知函数![]()
(1)若![]() ,求证:
,求证:![]()
(2)若![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)(﹣∞,0]
【解析】
(1)利用导数求x<0时,f(x)的极大值为![]() ,即证
,即证![]() (2)等价于k≤
(2)等价于k≤![]() ,x>0,令g(x)=
,x>0,令g(x)=![]() ,x>0,再求函数g(x)的最小值得解.
,x>0,再求函数g(x)的最小值得解.
(1)∵函数f(x)=x2e3x,∴f′(x)=2xe3x+3x2e3x=x(3x+2)e3x.
由f′(x)>0,得x<﹣![]() 或x>0;由f′(x)<0,得
或x>0;由f′(x)<0,得![]() ,
,
∴f(x)在(﹣∞,﹣![]() )内递增,在(﹣
)内递增,在(﹣![]() ,0)内递减,在(0,+∞)内递增,
,0)内递减,在(0,+∞)内递增,
∴f(x)的极大值为![]() ,
,
∴当x<0时,f(x)≤![]()
(2)∵x2e3x≥(k+3)x+2lnx+1,∴k≤![]() ,x>0,
,x>0,
令g(x)=![]() ,x>0,则g′(x)
,x>0,则g′(x)![]() ,
,
令h(x)=x2(1+3x)e3x+2lnx﹣1,则h(x)在(0,+∞)上单调递增,
且x→0+时,h(x)→﹣∞,h(1)=4e3﹣1>0,
∴存在x0∈(0,1),使得h(x0)=0,
∴当x∈(0,x0)时,g′(x)<0,g(x)单调递减,
当x∈(x0,+∞)时,g′(x)>0,g(x)单调递增,
∴g(x)在(0,+∞)上的最小值是g(x0)=![]() ,
,
∵h(x0)=![]() +2lnx0﹣1=0,所以
+2lnx0﹣1=0,所以![]() ,
,
令![]() ,
,
令![]()
所以![]() =1,
=1,![]() ,
,
∴g(x0)![]()
∴实数k的取值范围是(﹣∞,0].


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() ,其中,
,其中, ![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() 有
有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足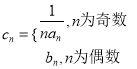 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:![]() ;
;![]() ;
;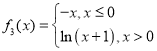 ;
;![]() .则其中是“偏对称函数”的函数个数为( )
.则其中是“偏对称函数”的函数个数为( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
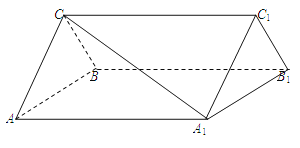
(Ⅰ)证明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C 与平面BB1C1C所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com