
| 2x-$\frac{π}{3}$ | -$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3}{2}π$ | $\frac{5}{3}π$ |
分析 (1)由条件根据余弦函数的周期性求得ω的值.
(2)由条件利用五点法作函数函数y=Acos(ωx+φ)在一个周期上的简图.
(3)结合函数f(x)的图象,可得它的减区间.
解答 解:(1)∵函数f(x)=cos(ωx-$\frac{π}{3}$)(ω>0)的最小正周期为$\frac{2π}{ω}$=π,
∴ω=2.
(2)列表:
| 2x-$\frac{π}{3}$ | -$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | $\frac{5π}{3}$ |
| x | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | π |
| f(x) | $\frac{1}{2}$ | 1 | 0 | -1 | 0 | 1 |
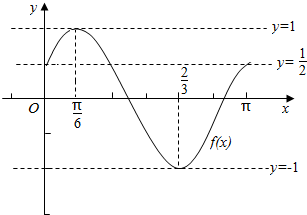
点评 本题主要考查余弦函数的周期性,用五点法作函数函数y=Acos(ωx+φ)在一个周期上的简图,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 观日出,赏瀑布,或是重温老别墅里的民国往事和《庐山恋》的柔美爱情,庐山每天都吸引大量的国内外游客,从山脚的A点徒步攀登到山顶O处的主景区,沿途风景秀丽,令人流连忘返,下图是一张登山的地图,若游客在每一个岔路口选择哪一条路线上山是等可能的(假定游客始终沿上山路线前进,不往下走,例如从F不能向D点走)
观日出,赏瀑布,或是重温老别墅里的民国往事和《庐山恋》的柔美爱情,庐山每天都吸引大量的国内外游客,从山脚的A点徒步攀登到山顶O处的主景区,沿途风景秀丽,令人流连忘返,下图是一张登山的地图,若游客在每一个岔路口选择哪一条路线上山是等可能的(假定游客始终沿上山路线前进,不往下走,例如从F不能向D点走) 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com