
分析 求出抛物线y=8x2-8nx-n2与坐标轴相交的三点为(0,-n2),($\frac{2-\sqrt{6}}{4}n,0$),($\frac{2+\sqrt{6}}{4}$n,0),设过这三点的圆的方程为x2+y2+Dx+Ey+F=0,利用待定系数法求出圆的方程为${x}^{2}+{y}^{2}-x+Ey-\frac{1}{4}$=0,由此能求出圆经过的定点的坐标.
解答 解:∵抛物线y=8x2-8nx-n2与坐标轴交于三点,
∴由x=0,得y=-n2,由y=0,得8x2-8nx-n2=0,
解得${x}_{1}=\frac{2+\sqrt{6}}{4}n$,${x}_{2}=\frac{2-\sqrt{6}}{4}$n,
∴抛物线y=8x2-8nx-n2与坐标轴相交的三点为(0,-n2),($\frac{2-\sqrt{6}}{4}n,0$),($\frac{2+\sqrt{6}}{4}$n,0),
设过这三点的圆的方程为x2+y2+Dx+Ey+F=0,
则$\left\{\begin{array}{l}{{n}^{4}-{n}^{2}E+F=0}\\{\frac{10-4\sqrt{6}}{16}+\frac{2-\sqrt{6}}{4}D+F=0}\\{\frac{10+4\sqrt{6}}{16}+\frac{2+\sqrt{6}}{4}D+F=0}\end{array}\right.$,解得D=-1,F=-$\frac{1}{4}$,
∴圆的方程为${x}^{2}+{y}^{2}-x+Ey-\frac{1}{4}$=0,
设该圆过定点P(x0,y0),
则${{x}_{0}}^{2}+{{y}_{0}}^{2}-{x}_{0}+E{y}_{0}-\frac{1}{4}$=0,
∵圆经过一个定点,∴y0=0,${{x}_{0}}^{2}-{x}_{0}-\frac{1}{4}=0$,
解得x0=$\frac{1±\sqrt{2}}{2}$,∴该定点坐标为($\frac{1±\sqrt{2}}{2}$,0).
故答案为:($\frac{1±\sqrt{2}}{2}$,0).
点评 本题考查圆经过的定点坐标的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6] | B. | [-8,-6) | C. | (-8,-6] | D. | [-8,-6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
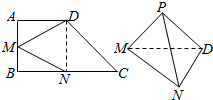 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$),k∈Z | B. | (kπ,(k+1)π),k∈Z | ||
| C. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$),k∈Z | D. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$),k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com