
| A. | 3020+$\sqrt{3}$ | B. | 3020+$\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{3}$+3018 | D. | 3018+$\frac{\sqrt{3}-1}{2}$ |
分析 根据数列的递推关系及其[x]、{x}的意义,求出数列的前几项,得到数列的规律性,即可得到结论.
解答 解:∵数列{an}满足a1=$\sqrt{3}$,an+1=[an]+$\frac{1}{\{{a}_{n}\}}$,
∴a2=1+$\frac{1}{\sqrt{3}-1}$=2+$\frac{\sqrt{3}-1}{2}$,同理可得:a3=4+($\sqrt{3}$-1),a4=5+$\frac{\sqrt{3}-1}{2}$,a5=7+($\sqrt{3}$-1),a6=8+$\frac{\sqrt{3}-1}{2}$,
a7=10+($\sqrt{3}$-1),a8=11+$\frac{\sqrt{3}-1}{2}$,a9=13+($\sqrt{3}$-1),….
∴a2n=(3n-1)+$\frac{\sqrt{3}-1}{2}$.
则a2014=3×1007-1+$\frac{\sqrt{3}-1}{2}$=3020+$\frac{\sqrt{3}-1}{2}$.
故选:B.
点评 本题考查了数列的递推关系、新定义、等差数列的通项公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a>1} | B. | {a|a≥1} | C. | {a|a≤1} | D. | {a|0≤a≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,0) | B. | (-4,0) | C. | (-∞,0) | D. | {-4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
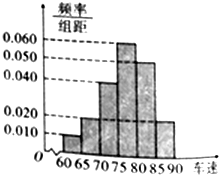 去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费
去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com