
| A. | (-5,0) | B. | (-4,0) | C. | (-∞,0) | D. | {-4} |
分析 先判断函数g(x)的取值范围,然后根据f(x)<0和g(x)<0至少有一个成立.则m的取值范围即可求出.
解答 解:∵g(x)=2x-4,当x≥2时,g(x)≥0,
又∵?x∈R,f(x)<0或g(x)<0,
∴f(x)=m(x-m)(x+m+3)<0在x≥2时恒成立,
即m(x-m)(x+m+3)<0在x≥2时恒成立,
则二次函数y=m(x-m)(x+m+3)图象开口只能向下,且与x轴交点都在(2,0)的左侧,
∴$\left\{\begin{array}{l}{m<0}\\{-m-3<2}\\{m<2}\end{array}\right.$,
解得-5<m<0,
∴实数m的取值范围是:(-5,0).
故选:A.
点评 本题主要考查指数函数和二次函数的图象和性质,根据条件确定f(x)=m(x-m)(x+m+3)<0在x≥2时恒成立是解决本题的关键,综合性较强,难度较大.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3020+$\sqrt{3}$ | B. | 3020+$\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{3}$+3018 | D. | 3018+$\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
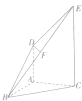 如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,
如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com