
分析 利用正弦定理化简已知不等式可得a2+b2<c2,进而利用余弦定理可求cosC<0,结合C的范围即可判断得解.
解答 解:△ABC中,由正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=k$>0,
∴sinA=$\frac{a}{k}$,sinB=$\frac{b}{k}$,sinC=$\frac{c}{k}$.
∵asinA+bsinB<csinC,
∴$\frac{{a}^{2}}{k}$+$\frac{{b}^{2}}{k}$<$\frac{{c}^{2}}{k}$,即a2+b2<c2.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$<0.
∵0<C<π,
∴$\frac{π}{2}$<C<π.
∴角C为钝角.
∴△ABC的形状是钝角三角形.
故答案为:钝角三角形.
点评 本题主要考查了正弦定理,余弦定理,余弦函数的图象和性质在解三角形中的应用,熟练掌握正弦定理和余弦定理是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,0) | B. | (-4,0) | C. | (-∞,0) | D. | {-4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
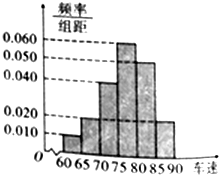 去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费
去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
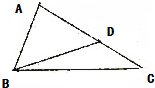 如图,在△ABC中,sin$\frac{∠ABC}{2}=\frac{{\sqrt{3}}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则cos∠ACB=$\frac{7}{9}$.
如图,在△ABC中,sin$\frac{∠ABC}{2}=\frac{{\sqrt{3}}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则cos∠ACB=$\frac{7}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com