
分析 (Ⅰ)求出导数,运用两角和的正弦公式化简,求出导数为0的根,讨论根附近的导数的符号相反,即可得到极值点,求得极值,运用等比数列的定义即可得证;
(Ⅱ)由sinφ=$\frac{1}{\sqrt{1+{a}^{2}}}$,可得对一切n∈N*,xn<|f(xn)|恒成立.即为nπ-φ<$\frac{1}{\sqrt{1+{a}^{2}}}$ea(nπ-φ)恒成立?$\frac{\sqrt{{a}^{2}+1}}{a}$<$\frac{{e}^{a(nπ-φ)}}{a(nπ-φ)}$,①设g(t)=$\frac{{e}^{t}}{t}$(t>0),求出导数,求得最小值,由恒成立思想即可得证.
解答 证明:(Ⅰ)f′(x)=eax(asinx+cosx)=$\sqrt{{a}^{2}+1}$•eaxsin(x+φ),
tanφ=$\frac{1}{a}$,0<φ<$\frac{π}{2}$,
令f′(x)=0,由x≥0,x+φ=mπ,即x=mπ-φ,m∈N*,
对k∈N,若(2k+1)π<x+φ<(2k+2)π,即(2k+1)π-φ<x<(2k+2)π-φ,
则f′(x)<0,因此在((m-1)π-φ,mπ-φ)和(mπ-φ,(m+1)π-φ)上f′(x)符号总相反.
于是当x=nπ-φ,n∈N*,f(x)取得极值,所以xn=nπ-φ,n∈N*,
此时f(xn)=ea(nπ-φ)sin(nπ-φ)=(-1)n+1ea(nπ-φ)sinφ,
易知f(xn)≠0,而$\frac{f({x}_{n+1})}{f({x}_{n})}$=$\frac{(-1)^{n+2}{e}^{a((n+1)π-φ)}sinφ}{(-1)^{n+1}{e}^{a(nπ-φ)}sinφ}$=-eaπ是常数,
故数列{f(xn)}是首项为f(x1)=ea(π-φ)sinφ,公比为-eaπ的等比数列;
(Ⅱ)由sinφ=$\frac{1}{\sqrt{1+{a}^{2}}}$,可得对一切n∈N*,xn<|f(xn)|恒成立.
即为nπ-φ<$\frac{1}{\sqrt{1+{a}^{2}}}$ea(nπ-φ)恒成立?$\frac{\sqrt{{a}^{2}+1}}{a}$<$\frac{{e}^{a(nπ-φ)}}{a(nπ-φ)}$,①
设g(t)=$\frac{{e}^{t}}{t}$(t>0),g′(t)=$\frac{{e}^{t}(t-1)}{{t}^{2}}$,
当0<t<1时,g′(t)<0,g(t)递减,当t>1时,g′(t)>0,g(t)递增.
t=1时,g(t)取得最小值,且为e.
因此要使①恒成立,只需$\frac{\sqrt{{a}^{2}+1}}{a}$<g(1)=e,
只需a>$\frac{1}{\sqrt{{e}^{2}-1}}$,当a=$\frac{1}{\sqrt{{e}^{2}-1}}$,tanφ=$\frac{1}{a}$=$\sqrt{{e}^{2}-1}$$>\sqrt{3}$,且0<φ<$\frac{π}{2}$,
可得$\frac{π}{3}$<φ<$\frac{π}{2}$,于是π-φ<$\frac{2π}{3}$<$\sqrt{{e}^{2}-1}$,且当n≥2时,nπ-φ≥2π-φ>$\frac{3π}{2}$>$\sqrt{{e}^{2}-1}$,
因此对n∈N*,axn=$\frac{nπ-φ}{\sqrt{{e}^{2}-1}}$≠1,即有g(axn)>g(1)=e=$\frac{\sqrt{{a}^{2}+1}}{a}$,
故①亦恒成立.
综上可得,若a≥$\frac{1}{\sqrt{{e}^{2}-1}}$,则对一切n∈N*,xn<|f(xn)|恒成立.
点评 本题考查导数的运用:求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
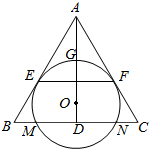 如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
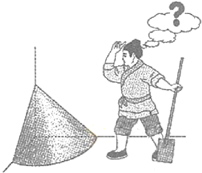 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )| A. | 14斛 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com