练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知等比数列{an}满足a1=$\frac{1}{4}$，a3a5=4（a4-1），则a2=（　　）
    A．2B．1C．$\frac{1}{2}$D．$\frac{1}{8}$

    分析 利用等比数列的通项公式即可得出．

    解答 解：设等比数列{an}的公比为q，
    ∵${a_1}=\frac{1}{4}$，a3a5=4（a4-1），
    ∴$（\frac{1}{4}）^{2}×{q}^{6}$=4$（\frac{1}{4}{q}^{3}-1）$，
    化为q3=8，解得q=2
    则a2=$\frac{1}{4}×2$=$\frac{1}{2}$．
    故选：C．

    点评 本题考查了等比数列的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知a＞0，函数f（x）=eaxsinx（x∈[0，+∞]）．记xn为f（x）的从小到大的第n（n∈N*）个极值点．证明：
    （Ⅰ）数列{f（xn）}是等比数列；
    （Ⅱ）若a≥$\frac{1}{\sqrt{{e}^{2}-1}}$，则对一切n∈N*，xn＜|f（xn）|恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．（x2+x+y）5的展开式中，x5y2的系数为（　　）
    A．10B．20C．30D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某同学将“五点法”画函数f（x）=Asin（wx+φ）（w＞0，|φ|＜$\frac{π}{2}$）在某一个时期内的图象时，列表并填入部分数据，如下表：
    wx+φ
    0    		$\frac{π}{2}$π$\frac{3π}{2}$2π
    x$\frac{π}{3}$$\frac{5π}{6}$
    Asin（wx+φ）05-50
    （1）请将上述数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；
    （2）将y=f（x）图象上所有点向左平移$\frac{π}{6}$个单位长度，得到y=g（x）图象，求y=g（x）的图象离原点O最近的对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，则A∪B=（　　）
    A．（-1，3）B．（-1，0）C．（0，2）D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

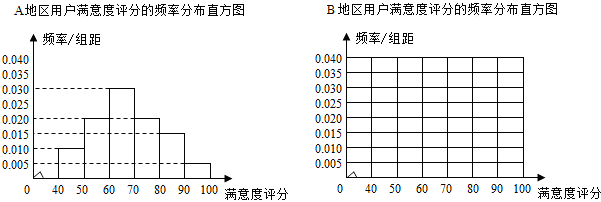
    16．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表

    B地区用户满意度评分的频数分布表
    满意度评分分组[50，60）[60，70）[70，80）[80，90）[90，100）
    频数2814106
    （1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）
    （Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：
    满意度评分低于70分70分到89分不低于90分
    满意度等级不满意满意非常满意
    估计哪个地区用户的满意度等级为不满意的概率大？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设x∈R，则“|x-2|＜1”是“x2+x-2＞0”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（　　）
    A．∠A′DB≤αB．∠A′DB≥αC．∠A′CB≤αD．∠A′CB≥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路和山区边界的直线型公路，记两条相互垂直的公路为l1，l2，山区边界曲线为C，计划修建的公路为l，如图所示，M，N为C的两个端点，测得点M到l1，l2的距离分别为5千米和40千米，点N到l1，l2的距离分别为20千米和2.5千米，以l2，l1在的直线分别为x，y轴，建立平面直角坐标系xOy，假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$（其中a，b为常数）模型．
    （1）求a，b的值；
    （2）设公路l与曲线C相切于P点，P的横坐标为t．
    ①请写出公路l长度的函数解析式f（t），并写出其定义域；
    ②当t为何值时，公路l的长度最短？求出最短长度．

    查看答案和解析>>

    同步练习册答案