【答案】
分析:(1)欲求实数a的值,只须求出切线斜率的值列出关于a的等式即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率,最后利用斜率为0即可求得a;
(2)求出函数的导数,讨论a的取值范围,再根据导数求函数的单调性,从而可求出函数的最小值;
(3)欲使y=kx与y=f(x)的图象存在三个交点,只需kx=e
x(x
2-2x-2)有三解,将k分离,研究另一侧函数的图象性质,结合图象可求出k的取值范围.
解答: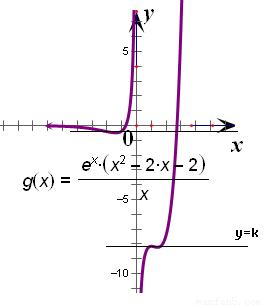
解:(1)f′(x)=(e
x)′•(ax
2-2x-2)+e
x•(ax
2-2x-2)′
=e
x•(ax
2-2x-2)+e
x•(2ax-2)
=a•e
x•(x-
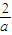
)(x+2).
∵曲线y=f(x)在点P(2,f(2))处的切线垂直于y轴,
由导数的几何意义得f′(2)=0,
∴a=1.
∴实数a的值为:1.
(2)由(1)可知设|sinx|=t,(0≤t≤1),则转化为求函数y=f(t),(0≤t≤1)的最小值.
∵a>0∴f′(x)=e
x•[ax
2+(2a-2)x-4]=a•e
x•(x-
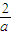
)(x+2).
令f′(x)=0,解得x=
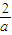
或x=-2(舍).
若
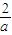
≥1,即0<a≤2时,x∈[0,1]时,f′(x)<0,
函数f(t)在[0,1]上为减函数则函数f(t)的最小值为f(1)=(a-4)e;
若0<
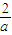
<1,即a>2时,函数f(t)在(0,
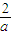
)上递减,在(
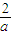
,1)上递增
∴函数f(t)的最小值为f(
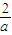
)=-2
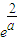
∴当0<a≤2时,函数f(|sinx|)的最小值为(a-4)e
当a>2时,函数f(|sinx|)的最小值为-2
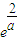
(3)∵y=kx与y=f(x)的图象存在三个交点
∴kx=e
x(x
2-2x-2)有三解,即k=
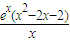
而令g(x)=
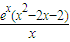
则g′(x)=
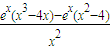
=
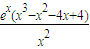
.
令g′(x)=0解得x=1或2或-2
当x<-2时,g′(x)<0,当-2<x<0时,g′(x)>0,
当0<x<1时,g′(x)>0,当1<x<2时,g′(x)<0,当x>2时,g′(x)>0
∴当x=-2时函数取极小值g(-2)=-3e
-2,当x=1时,函数取极大值g(1)=-3e,
当x=2时,函数取极小值g(2)=-e
2,画出函数图象
结合函数的图象可知-e
2<k<-3e或-3e
-2<k<0
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的极值,同时考查了转化的思想和运算求解的能力,属于难题.

 解:(1)f′(x)=(ex)′•(ax2-2x-2)+ex•(ax2-2x-2)′
解:(1)f′(x)=(ex)′•(ax2-2x-2)+ex•(ax2-2x-2)′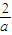 )(x+2).
)(x+2).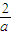 )(x+2).
)(x+2).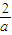 或x=-2(舍).
或x=-2(舍).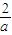 ≥1,即0<a≤2时,x∈[0,1]时,f′(x)<0,
≥1,即0<a≤2时,x∈[0,1]时,f′(x)<0,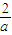 <1,即a>2时,函数f(t)在(0,
<1,即a>2时,函数f(t)在(0,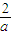 )上递减,在(
)上递减,在(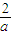 ,1)上递增
,1)上递增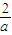 )=-2
)=-2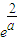
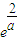
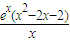
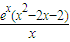 则g′(x)=
则g′(x)=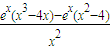 =
=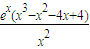 .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案