
数列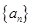 满足
满足
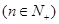 。
。
(Ⅰ)若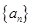 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若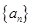 满足
满足 ,
,  为
为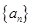 的前
的前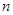 项和,求
项和,求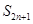 。
。
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
(本小题满分14分)
已知函数![]() 。
。
(1)证明:![]()
(2)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(3)设数列![]() 满足:
满足:![]() ,设
,设![]() ,
,
若(2)中的![]() 满足对任意不小于2的正整数
满足对任意不小于2的正整数![]() ,
,![]() 恒成立,
恒成立,
试求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(13分)已知数列![]() 满足
满足![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,设
,设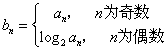 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)是否存在实数![]() ,使数列
,使数列![]() 满足不等式
满足不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州市番禺区高二下学期期中考试数学(理) 题型:解答题
(14分)已知数列 是首项
是首项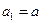 ,公差为2的等差数列,数列
,公差为2的等差数列,数列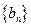 满足
满足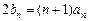 ;
;
(1)若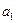 、
、 、
、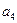 成等比数列,求数列
成等比数列,求数列 的通项公式;
的通项公式;
(2)若对任意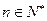 都有
都有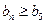 成立,求实数
成立,求实数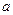 的取值范围;
的取值范围;
(3)数列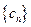 满足
满足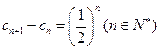 ,其中
,其中 ,
,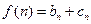 ,当
,当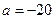 时,求
时,求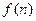 的最小值(
的最小值(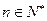 ).
).
查看答案和解析>>
科目:高中数学 来源:2014届浙江省杭州市高一5月月考数学试卷(解析版) 题型:填空题
下列命题:① 函数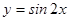 的单调增区间是[
的单调增区间是[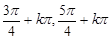 ],(k∈Z)② 函数
],(k∈Z)② 函数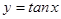 在
在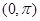 内是增函数③若数列
内是增函数③若数列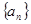 满足
满足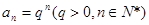 ,则
,则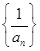 是等比数列;④若数列
是等比数列;④若数列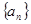 满足
满足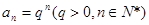 则
则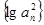 是等差数列; ⑤函数
是等差数列; ⑤函数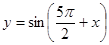 是偶函数,其中正确的命题序号是
是偶函数,其中正确的命题序号是
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省西安市高三下学期第一次模拟考试理科数学 题型:解答题
(本小题满分14分)
已知函数f(x)= x
x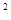 -ax
+ (a-1)
-ax
+ (a-1) ,
, .
.
(I)讨论函数 的单调性;
的单调性;
(II)若 ,数列
,数列 满足
满足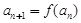 .
.
(1) 若首项 ,证明数列
,证明数列 为递增数列;
为递增数列;
(2) 若首项为正整数,数列 递增,求首项的最小值.
递增,求首项的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com