
分析 (1)令$\frac{x}{3}$=X,$\frac{y}{2}$=Y,由题设条件知,再由(a,b)是函数y=g(x)的图象上的点,即可得到函数y=g(x)的解析式;
(2)结合题意得到关于x的不等式组,解出即可.
解答 解:(1)令$\frac{x}{3}=X,\frac{y}{2}=Y$,所以x=3X,y=2Y,
因为点(x,y)是函数y=f(x)的图象上,
所以$2Y=log_2^{(3X+1)}$,即$Y=\frac{1}{2}log_2^{(3X+1)}$
所以$g(x)=\frac{1}{2}log_2^{(3x+1)}(x>-\frac{1}{3})$;
(2)由g(x)≥f(x),得$\frac{1}{2}log_2^{(3x+1)}≥log_2^{(x+1)}$,
所以$\left\{\begin{array}{l}3x+1>0\\ x+1>0\\ 3x+1≥{(x+1)^2}\end{array}\right.$解得0≤x≤1.
点评 本题考查的知识点是对数函数的图象与性质的综合应用,关键是根据基本不等式,求出真数的范围,进而根据对数函数的单调性解决问题,是一道基础题.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
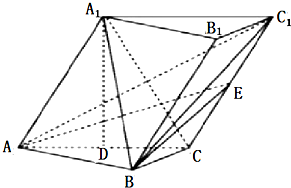 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1,CC1的中点为E.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1,CC1的中点为E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{12}{13}$ | B. | $\frac{12}{13}$ | C. | $±\frac{5}{13}$ | D. | -$\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 80 | 110 | 135 | 135 | 140 |
| 乙 | 100 | x | y | 125 | 155 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com