
| 甲 | 80 | 110 | 135 | 135 | 140 |
| 乙 | 100 | x | y | 125 | 155 |
分析 (1)由平均数═120求x,再求方差比较可得稳定性;
(2)由已知得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望.
解答 解:(1)∵由$\overline{{x}_{甲}}$=$\frac{80+110+135+135+140}{5}$=120,
∴$\overline{{x}_{乙}}$=$\frac{100+x+y+125+155}{5}$=120,可得:y=220-x,
∴S2甲=$\frac{1}{5}$[(80-120)2+(110-120)2+(135-120)2+(135-120)2+(140-120)2]=310;
S2乙=$\frac{1}{5}$[(100-120)2+(x-120)2+(y-120)2+(125-120)2+(155-120)2]=330+$\frac{2[(x-110)^{2}+100]}{5}$;
∴当x=110,y=110时,乙品牌汽车CO2排放量的稳定性最好.
(2)由已知得X的可能取值为0,1,2,3.
P(X=0)=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}×\frac{{C}_{4}^{2}}{{C}_{5}^{2}}$=$\frac{3}{50}$
P(X=1)=$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}×\frac{{C}_{4}^{2}}{{C}_{5}^{2}}$+$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}×\frac{{C}_{4}^{1}{C}_{1}^{1}}{{C}_{5}^{2}}$=$\frac{11}{50}$
P(X=2)=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}×\frac{{C}_{4}^{2}}{{C}_{5}^{2}}$+$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}×\frac{{C}_{4}^{1}}{{C}_{5}^{2}}$=$\frac{21}{50}$,
P(X=3)=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}×\frac{{C}_{4}^{1}}{{C}_{5}^{2}}$=$\frac{6}{50}$;
则X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{3}{50}$ | $\frac{20}{50}$ | $\frac{21}{50}$ | $\frac{6}{50}$ |
点评 本题考查了数据的分析与应用,同时考查了古典概型在实际问题中的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 (文)如图矩形ABCD所在的平面与三角形CDE所在的平面交于CD,AE⊥平面CDE.
(文)如图矩形ABCD所在的平面与三角形CDE所在的平面交于CD,AE⊥平面CDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
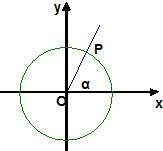 已知角α的终边与单位圆的交点是P(x0,y0)
已知角α的终边与单位圆的交点是P(x0,y0)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
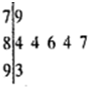 某学校在五四青年节举办十佳歌手赛.如图是七位评委为某选手打出的分数的茎叶图(茎表示十位上的数字,叶表示个位上的数字),去掉一个最高分和一个最低分后,所剩数据的平均数与方差分别为( )
某学校在五四青年节举办十佳歌手赛.如图是七位评委为某选手打出的分数的茎叶图(茎表示十位上的数字,叶表示个位上的数字),去掉一个最高分和一个最低分后,所剩数据的平均数与方差分别为( )| A. | 83; 1.6 | B. | 85; 1.5 | C. | 85; 1.6 | D. | 86; 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,9) | B. | (-4,-9) | C. | (4,-9) | D. | (-4,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
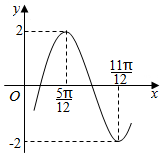 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com