
分析 (Ⅰ)求出函数f(x)的导数,通过讨论a的范围求出函数的单调区间即可;
(Ⅱ)法一:问题转化为证明ex-lnx-1>0,设g(x)=ex-lnx-1(x>0),问题转化为证明?x>0,g(x)>0,根据函数的单调性证明即可;
法二:问题转化为证明x-1≥lnx(x>0),令h(x)=x-1-lnx(x>0),根据函数的单调性证明即可.
解答 解:(Ⅰ)当b=1时,$f(x)=\frac{1}{2}a{x^2}-(1+{a^2})x+alnx$$f'(x)=ax-(1+{a^2})+\frac{a}{x}=\frac{(ax-1)(x-a)}{x}$…(1分)
讨论:1°当a≤0时,$x-a>0,\frac{1}{x}>0,ax-1<0⇒f'(x)<0$
此时函数f(x)的单调递减区间为(0,+∞),无单调递增区间 …(2分)
2°当a>0时,令$f'(x)=0⇒x=\frac{1}{a}$或a
①当$\frac{1}{a}=a(a>0)$,¼?a=1?±£?此时$f'(x)=\frac{{{{(x-1)}^2}}}{x}≥0(x>0)$
此时函数f(x)单调递增区间为(0,+∞),无单调递减区间 …(3分)
②当$0<\frac{1}{a}<a$,即a>1时,此时在$(0,\frac{1}{a})$和(a,+∞)上函数f'(x)>0,
在$(\frac{1}{a},a)$上函数f'(x)<0,此时函数f(x)单调递增区间为$(0,\frac{1}{a})$和(a,+∞);
单调递减区间为$(\frac{1}{a},a)$…(4分)
③当$0<a<\frac{1}{a}$,即0<a<1时,此时函数f(x)单调递增区间为(0,a)和$(\frac{1}{a},+∞)$;
单调递减区间为$(a,\frac{1}{a})$…(6分)
(Ⅱ)证明:(法一)当a=1时 f(x)+ex>x2+x+1
只需证明:ex-lnx-1>0设g(x)=ex-lnx-1(x>0)
问题转化为证明?x>0,g(x)>0
令$g'(x)={e^x}-\frac{1}{x}$,$g''(x)={e^x}+\frac{1}{x^2}>0$,
∴$g'(x)={e^x}-\frac{1}{x}$为(0,+∞)上的增函数,且$g'(\frac{1}{2})=\sqrt{e}-2<0,g'(1)=e-1>0$…(8分)
∴存在惟一的${x_0}∈(\frac{1}{2},1)$,使得g'(xo)=0,${e^{x_0}}=\frac{1}{x_0}$,
∴g(x)在(0,x0)上递减,在(x0,+∞)上递增…(10分)
∴$g{(x)_{min}}=g({x_0})={e^{x_o}}-ln{x_{_0}}-1=\frac{1}{x_0}+{x_0}-1≥2-1=1$,
∴g(x)min>0∴不等式得证 …(12分)
(法二)先证:x-1≥lnx(x>0)
令h(x)=x-1-lnx(x>0)∴$h'(x)=1-\frac{1}{x}=\frac{x-1}{x}=0⇒x=1$,
∴h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴h(x)min=h(1)=0,∴h(x)≥h(1)⇒x-1≥lnx…(8分)
∴1+lnx≤1+x-1=x⇒ln(1+x)≤x,
∴eln(1+x)≤ex…(10分),
∴ex≥x+1>x≥1+lnx,
∴ex>1+lnx
故ex-lnx-1>0,证毕 …(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查不等式的证明,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2017 | C. | 2016 | D. | 4034 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-e,e) | C. | (-1,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
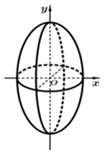 祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于$\frac{4}{3}π×{b^2}a$.
祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于$\frac{4}{3}π×{b^2}a$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 99 | B. | 90 | C. | 84 | D. | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈({0,+∞}),lnx≥2\frac{x-1}{x+1}$ | B. | $?{x_0}∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ | ||
| C. | $?x∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ | D. | 不存在${x_0}∈({0,+∞}),lnx<2\frac{x-1}{x+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com