
| A�� | ��-�ޣ�0�� | B�� | ��-e��e�� | C�� | ��-1��1�� | D�� | ��0��+�ޣ� |
���� ������ɵ�f��f��x����=2����5���⣬��t=f��x����f��t��=2����x��0ʱ�����õ��������������ֵ���õ�f��t��=2��[1��+�ޣ���2���⣬
����x��0ʱ�����ݺ�������㣨0��3�����������ۣ����������k��0ʱ��f��t��=2ʱ��3���⣬������Խ����
��� 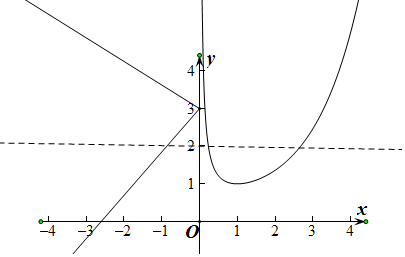 �⣺����f��x��Ϊ������5�⡰��
�⣺����f��x��Ϊ������5�⡰��
��f��f��x����=2����5���⣬
��t=f��x����
��f��t��=2��
�ߵ�x��0ʱ��f��x��=$\frac{{e}^{x}}{ex}$=$\frac{{e}^{x-1}}{x}$��
��f��x��=$\frac{{e}^{x-1}��x-1��}{{x}^{2}}$��
��0��x��1ʱ��f�䣨x����0������f��x�������ݼ���
��x��1ʱ��f�䣨x����0������f��x������������
��f��x��min=f��1��=1��
��t��1��
��f��t��=2��[1��+�ޣ���2���⣬
��x��0ʱ��f��x��=kx+3������f��x������㣨0��3����
��k��0ʱ��f��x����f��0��=3��
��t��3
��f��3��=$\frac{{e}^{2}}{3}$��2��
��f��t��=2��[3��+�ޣ����⣬
��k��0ʱ��f��x����f��0��=3��
��f��t��=2���ڣ�0��3]����2���⣬�ڣ��ޣ�0]����1���⣬
��������f��f��x����=2��k��0ʱ����5���⣬
��ѡ��D
���� ���⿼�����¶����Ӧ���Լ������Ľ�������Լ������ͺ�������ֵ���⣬�ؼ������f��t���Ķ������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���PA=AD=2��$BD=2\sqrt{2}$��E��F�ֱ�ΪAD��PC�е㣮
��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���PA=AD=2��$BD=2\sqrt{2}$��E��F�ֱ�ΪAD��PC�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
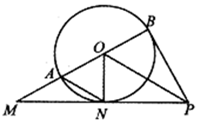 ��ͼ��ʾ����֪ABΪ��O��ֱ����PB��PN���ǡ�O�����ߣ��е�ֱ�ΪB��N��PN��BA���ӳ����ڵ�M��
��ͼ��ʾ����֪ABΪ��O��ֱ����PB��PN���ǡ�O�����ߣ��е�ֱ�ΪB��N��PN��BA���ӳ����ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0�� | B�� | ��-e��e�� | C�� | ��-1��1�� | D�� | ��0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ȴ�ʱ��T1�����ӣ� | 1 | 2 | 3 | 4 | 5 |
| Ƶ�� | 1500 | 1000 | 500 | 500 | 1500 |
| ����ȴ�ʱ��T2�����ӣ� | 1 | 2 | 3 | 4 | 5 |
| Ƶ�� | 1000 | 500 | 2000 | 1250 | 250 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | 10 | C�� | -20 | D�� | 20 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com