
分析 (Ⅰ)求出函数f′(x)的解析式,通过讨论a的范围,求出方程f′(x)=0的零点个数即可;
(Ⅱ)对于任意的x1,x2∈[0,2],不等式m-am2≥|f(x1)-f(x2)|恒成立,等价于m-am2≥|f(x1)-f(x2)|max,由( I)易求f(x)的最大值、最小值,从而可得|f(x1)-f(x2)|max,进而问题转化为对于任意的a∈[-3,0],m-am2≥5-3a恒成立,构造关于a的一次函数g(a)=(m2-3)a-m+5,a∈[-3,0],只需$\left\{\begin{array}{l}{g(-3)≤0}\\{g(0)≤0}\end{array}\right.$,解出即可.
解答 解:(Ⅰ)f'(x)=6x2-6(a+1)x+6a=6(x-1)(x-a),
a<-1时,令f′(x)=0,解得:x=1,f′(x)有1个零点,
-1≤a<1时,令f′(x)=0,解得:x=a,1,f′(x)2个零点,
a=1时,令f′(x)=0,解得:x=1,f′(x)有1个零点,
1<a≤3时,令f′(x)=0,解得:x=a,1,f′(x)2个零点,
a>3时,令f′(x)=0,解得:x=1,f′(x)有1个零点;
(Ⅱ)对于任意的x1,x2∈[0,2],
不等式m-am2≥|f(x1)-f(x2)|恒成立,
等价于m-am2≥|f(x1)-f(x2)|max,
f'(x)=6x2-6(a+1)x+6a=6(x-1)(x-a),
当a≤0时,由f'(x)>0,得x<a或x>1,由f'(x)<0,得a<x<a,
∴f(x)的增区间为(-∞,a),(1,+∞),减区间为(a,1);
故f(x)在[0,1]上单调递减,
在[1,2]上单调递增,且f(0)=0,f(2)=4,
∴|f(x1)-f(x2)|max=f(2)-f(1)=5-3a,
则问题转化为对于任意的a∈[-3,0],m-am2≥5-3a恒成立,
即对于任意的a∈[-3,0],(m2-3)a-m+5≤0恒成立.
构造g(a)=(m2-3)a-m+5,a∈[-3,0],
只需 $\left\{\begin{array}{l}{g(-3)≤0}\\{g(0)≤0}\end{array}\right.$,解得m∈[5,+∞),
∴实数m的取值范围是[5,+∞).
点评 本题考查利用导数研究函数的单调性、在闭区间上的最值求解及恒成立问题,考查转化思想,考查学生分析解决问题的能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{3}{2}$ | B. | ±$\frac{2}{3}$ | C. | ±$\frac{3}{4}$ | D. | ±$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50万元 | B. | 30万元 | C. | 25万元 | D. | 22万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
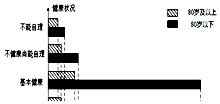 我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | $\frac{68}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2017 | C. | 2016 | D. | 4034 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-e,e) | C. | (-1,1) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com