
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由题意可得f(-x)=f(x),利用出公式可得:sinx$cos(θ+\frac{π}{3})$=0,上式对于任意实数x∈R都成立,可得cosθ=0,θ∈[-$\frac{π}{2}$,$\frac{π}{2}}]}$],即可得出.
解答 解:∵函数f(x)=sin(x+θ)+$\sqrt{3}$cos(x+θ)(θ∈[-$\frac{π}{2}$,$\frac{π}{2}}]}$])是偶函数,
∴f(-x)=f(x),∴f(-x)=sin(-x+θ)+$\sqrt{3}$cos(-x+θ)=sin(x+θ)+$\sqrt{3}$cos(x+θ),
∴sinxcosθ+$\sqrt{3}$sinxsinθ=0,
∴2sinx$cos(θ+\frac{π}{3})$=0,
上式对于任意实数x∈R都成立,∴cosθ=0,θ∈[-$\frac{π}{2}$,$\frac{π}{2}}]}$],
∴$θ=\frac{π}{6}$.
故选:B.
点评 本题考查了函数的奇偶性、和差公式,考查了推理能力与计算能力,属于中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{{\sqrt{2}}}{2},0$] | B. | [-1,0] | C. | [-$\sqrt{2},0$] | D. | [-$\sqrt{3},0$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (-∞,0] | C. | (-∞,0]∪[1,2] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
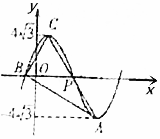 已知函数f(x)=4$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在平面直角坐标系中的部分图象如图所示,若∠ABC=90°,则ω=( )
已知函数f(x)=4$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在平面直角坐标系中的部分图象如图所示,若∠ABC=90°,则ω=( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com