
【题目】已知椭圆的长轴长为6,离心率为 ![]() ,F2为椭圆的右焦点.
,F2为椭圆的右焦点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)点M在圆x2+y2=8上,且M在第一象限,过M作圆x2+y2=8的切线交椭圆于P,Q两点,判断△PF2Q的周长是否为定值并说明理由.
【答案】解:(I)根据已知,设椭圆的标准方程为 ![]() , ∴2a=6,a=3,
, ∴2a=6,a=3, ![]() ,c=1;
,c=1;
b2=a2﹣c2=8,![]()
(II)△PF2Q的周长是定值,
设P(x1 , y1),Q(x2 , y2),则 ![]() ,
,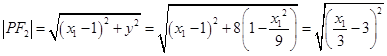 ,
,
∵0<x1<3,
∴ ![]() ,
,
在圆中,M是切点,
∴ 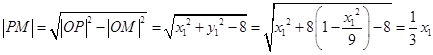 ,
,
∴ ![]() ,
,
同理|QF2|+|QM|=3,
∴|F2P|+|F2Q|+|PQ|=3+3=6,
因此△PF2Q的周长是定值6
【解析】(Ⅰ)由题意可知:2a=6, ![]() ,求得a和c的值,由b2=a2﹣c2 , 求得b,写出椭圆方程;(Ⅱ)设P(x1 , y1),Q(x2 , y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2﹣|OM|2 , 可得
,求得a和c的值,由b2=a2﹣c2 , 求得b,写出椭圆方程;(Ⅱ)设P(x1 , y1),Q(x2 , y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2﹣|OM|2 , 可得 ![]() ,同理|QF2|+|QM|=3,即可证明;
,同理|QF2|+|QM|=3,即可证明;


科目:高中数学 来源: 题型:
【题目】已知定义在区间[﹣3,3]上的单调函数f(x)满足:对任意的x∈[﹣3,3],都有f(f(x)﹣2x)=6,则在[﹣3,3]上随机取一个实数x,使得f(x)的值不小于4的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 点A({2,
=1(a>b>0)的左、右焦点分别为F1 , F2 , 点A({2, ![]() )在椭圆上,且满足
)在椭圆上,且满足 ![]()
![]() =0. (Ⅰ)求椭圆C的标准方程;
=0. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)动直线l:y=kx+m与椭圆C交于P,Q两点,且OP⊥OQ,是否存在圆x2+y2=r2使得l恰好是该圆的切线,若存在,求出r;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D=  ,给出下列四个命题: P1:(x,y)∈D,x+y+1≥0;
,给出下列四个命题: P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 且
且![]() ,设
,设![]() .
.
![]() 若
若![]() 2,3,4,5,
2,3,4,5,![]() 和
和![]() 2,3,4,5,
2,3,4,5,![]() ,分别求S的值;
,分别求S的值;
![]() 若集合A中所有元素之和为55,求S的最小值;
若集合A中所有元素之和为55,求S的最小值;
![]() 若集合A中所有元素之和为103,求S的最小值.
若集合A中所有元素之和为103,求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.
(1)若点C的坐标为(2, ![]() ),求a,b的值;
),求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() =
= ![]()
![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平和消费观念的转变,“三品一标”(无公害农产品、绿色食品、有机食品和农产品地理标志)已成为不少人的选择,为此某品牌植物油企业成立了有机食品快速检测室,假设该品牌植物油每瓶含有机物A的概率为p(0<p<1),需要通过抽取少量油样化验来确定该瓶油中是否含有有机物A,若化验结果呈阳性则含A,呈阴性则不含A.若多瓶该种植物油检验时,可逐个抽样化验,也可将若干瓶植物油的油样混在一起化验,仅当至少有一瓶油含有有机物A时混合油样呈阳性,若混合油样呈阳性,则该组植物油必须每瓶重新抽取油样并全部逐个化验.
(1)若 ![]() ,试求3瓶该植物油混合油样呈阳性的概率;
,试求3瓶该植物油混合油样呈阳性的概率;
(2)现有4瓶该种植物油需要化验,有以下两种方案: 方案一:均分成两组化验;方案二:混在一起化验;请问哪种方案更适合(即化验次数的期望值更小),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣(2a﹣1)x﹣lnx.
(1)当a>0时,求函数f(x)的单调递增区间;
(2)当a<0时,求函数f(x)在 ![]() 上的最小值;
上的最小值;
(3)记函数y=f(x)的图象为曲线C,设点A(x1 , y1),B(x2 , y2)是曲线C上的不同两点,点M为线段AB的中点,过点M作x轴的垂直交曲线C于点N,判断曲线C在点N处的切线是否平行于直线AB,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com