
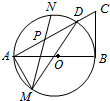
 如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4
如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4分析 (Ⅰ)利用切割线定理、相交弦定理,即可求MP•NP的值
(Ⅱ)证明∠C=∠DBA,∠DBA=∠AMD,即可证明∠C=∠AMD.
解答  (Ⅰ)解:因为BC为圆O的切线,所以BC2=CD•AC,
(Ⅰ)解:因为BC为圆O的切线,所以BC2=CD•AC,
因为BC=6,CD=4
所以AC=9,
所以AD=5,
因为P为AD的中点,
所以AP=PD=$\frac{5}{2}$
所以MP•NP=AP•PD=$\frac{25}{4}$
(Ⅱ)证明:连接BD,则∠ABC=90°,
所以∠C+∠CAB=90°,
因为AB为直径,
所以∠ADB=90°,
所以∠CAB+∠DBA=90°,
所以∠C=∠DBA,
因为∠DBA=∠AMD,
所以∠C=∠AMD.
点评 本题考查切割线定理、相交弦定理,考查学生分析解决问题的能力,正确运用切割线定理、相交弦定理是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)
现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com