
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 对于命题p,先求导,在令导数等于0,得到△=a2-4>0,求出a的范围,对于命题q,根据幂函数为增函数,得到指数大于0,再根据条件之间关系即可判断.
解答 解:命题p:∵函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+x有两个极值点,
∴f′(x)=x2+ax+1=0有不相等的实根,
∴△=a2-4>0,
解得-2<a<2,
命题q:函数g(x)=x${\;}^{{a}^{2}-a}$在(0,+∞)上为增函数,
∴a2-a>0,
解得a>0,或a<1,
∴p推不出q,q推不出p,
∴p是q的既不充分也不必要条件,
故选:D.
点评 本题考查了导数和函数的极值点,以及幂函数的性质,和充分必要条件,属于中档题.


科目:高中数学 来源: 题型:选择题
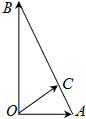
| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $\frac{21}{3}$ | C. | $\frac{67}{6}$ | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
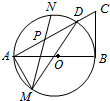 如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4
如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com