
 现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)
现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答) 分析 通过分析题目给出的图形,可知要完成给图中A、B、C、D四个区域进行染色,最少需要2种颜色,利用排列组合知识求解该种染法的方法种数,最后利用分类加法求和.
解答 解:完成给图中A、B、C、D四个区域进行染色,最少需要2种颜色,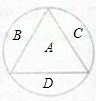
若使用两种颜色,则A,B,C三个区域同色,共有${{C}_{4}^{2}}_{\;}^{\;}{A}_{2}^{2}$=12种不同染色方法;
若使用三种颜色,则A,B,C有两个区域同色,共有${{C}_{4}^{3}C}_{3}^{2}{A}_{3}^{3}$=72种不同染色方法;
若使用四种颜色,共有${A}_{4}^{4}$=24种不同染色方法;
共有12+72+24=108种不同的染色方法,
故答案为:108.
点评 本题考查了排列、组合、及简单的计数问题,解答的关键是正确分类,明确相邻的两区域不能染相同的颜色,该题是中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | 6:3:2 | B. | 3:2:6 | C. | 2:6:3 | D. | 6:2:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
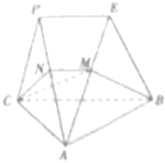 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
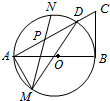 如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4
如图,AB为圆O的直径,BC为圆O的切线,连结AC交圆O于D,P为AD的中点,过P作不同于AD的弦交圆O于M、N两点,若BC=6,CD=4查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com