
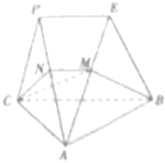
 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.分析 (Ⅰ)由PE∥CB,得BC∥平面APE,由此能证明MN∥PE.
(Ⅱ)由MN∥BC,得C、B、M、N共面,∠NCA为二面角N-CB-A的平面角,由此确定点N的位置.
解答 (1)证明:因为PE∥CB,所以BC∥平面APE …(3分)
又依题意平面ABC交平面APE于MN,
故MN∥BC,
所以MN∥PE.…(6分)
(2)解:由(1)知MN∥BC,故C、B、M、N共面,
平面ABC与平面MNC所成的锐二面角即N-CB-A.
因为平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,且CB⊥AC,
所以CB⊥平面PAC.故CB⊥CN,
故∠NCA为二面角N-CB-A的平面角…(10分)
所以∠NCA=30°.
所以CN⊥PA.
所以N是PA的中点.…(14分)
点评 本题考查直线与直线平行的证明,考查使锐二面角的大小为30°的点N的位置,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)
现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com