
分析 把原式变形,然后分析使两个展开式中乘积出现x2项的项,求乘积作和求得答案.
解答 解:由($\sqrt{x}$+1)4($\sqrt{x}$-1)8 =(x-1)4($\sqrt{x}$-1)4 ,
∴展开式中含x2的项为:
${C}_{4}^{2}{x}^{2}•{C}_{4}^{4}(\sqrt{x})^{0}(-1)^{4}+{C}_{4}^{3}x•(-1)^{3}•{C}_{4}^{2}(\sqrt{x})^{2}(-1)^{2}$$+{C}_{4}^{4}{x}^{0}•{C}_{4}^{0}(\sqrt{x})^{4}$=6x2-24x2+x2=-17x2.
∴($\sqrt{x}$+1)4($\sqrt{x}$-1)8的展开式中x2的系数为-17.
故答案为:-17.
点评 本题考查了二项式系数的性质,考查学生的计算求解能力,是基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
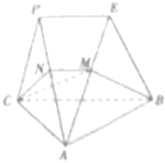 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com