
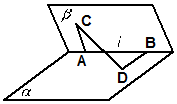
 如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )| A. | $\sqrt{11}$ | B. | $\sqrt{14}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{23}$ |
分析 由已知可得$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AB}$+$\overrightarrow{BD}$,利用数量积的性质即可得出.
解答 解:∵CA⊥AB,BD⊥AB,∴$\overrightarrow{CA}•\overrightarrow{AB}$=$\overrightarrow{BD}•\overrightarrow{AB}$=0,
∵<$\overrightarrow{AC}$,$\overrightarrow{BD}$>=60°,∴<$\overrightarrow{CA}$,$\overrightarrow{BD}$>=120°
∵$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AB}$+$\overrightarrow{BD}$,
∴$\overrightarrow{CD}$2=$\overrightarrow{CA}$2+$\overrightarrow{AB}$2+$\overrightarrow{BD}$2+2$\overrightarrow{CA}$•$\overrightarrow{AB}$+2$\overrightarrow{CA}$•$\overrightarrow{BD}$+2$\overrightarrow{AB}$•$\overrightarrow{BD}$=22+22+32+0+2×2×3×cos120°+0=11,
∴CD=$\sqrt{11}$.
故选A.
点评 熟练掌握向量的运算和数量积运算是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com