
分析 (Ⅰ)利用距离公式求出a,离心率求出c,得到b后即可求出椭圆方程.
(Ⅱ)法一:设A(x1,y1),B(x2,y2),①当直线l的斜率不存在时,求解点O到直线AB的距离.②当直线l的斜率存在时,设其方程为l:y=kx+m.联立直线与椭圆方程,利用韦达定理结合数量积,求出m,k关系式,然后求解距离即可.
法二:设A(x1,y1),B(x2,y2),①当直线l的斜率为0时,求解点O到直线AB的距离,②当直线l的斜率不为0,或斜率不存在时,设其方程为l:x=my+c.联立直线与椭圆方程,利用韦达定理以及数量积,求解距离即可.
(Ⅲ)法一:当直线OA、直线OB中有一条斜率不存在,另一条斜率为0时,易知S=1;当直线OA、直线OB斜率存在且不为0时,设直线OA的斜率为k,则直线OB的斜率为$-\frac{1}{k}$,利用平方差法以及弦长公式表示三角形的面积,利用基本不等式求出最值.
法二:由(Ⅱ),①当直线l的斜率不存在时,求出面积;②当直线l的斜率存在时,求出写出以及点到直线的距离,得到面积的表达式,利用二次函数的性质求解面积的最值.
解答 (本小题满分12分)
解:(Ⅰ)由已知,$\frac{|-a-2|}{{\sqrt{5}}}=\frac{4}{{\sqrt{5}}}⇒a=2$…(1分)
因为$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}⇒c=\sqrt{3}⇒{b^2}={a^2}-{c^2}=1$…(2分)
故所求椭圆的方程为$\frac{x^2}{4}+{y^2}=1$…(3分)
(Ⅱ)法一:设A(x1,y1),B(x2,y2),
①当直线l的斜率不存在时,由椭圆对称性知x1=x2,y1=-y2,因为以AB为直径的圆经过坐标原点O,故$\overrightarrow{OA}•\overrightarrow{OB}=0⇒{x_1}{x_2}+{y_1}{y_2}=0$,即${x_1}^2-{y_1}^2=0$
又因为点A(x1,y1)在椭圆上,故$\frac{{{x_1}^2}}{4}+{y_1}^2=1$,解得$|{x_1}|=|{y_1}|=\frac{{2\sqrt{5}}}{5}$,
此时点O到直线AB的距离为$d=\frac{{2\sqrt{5}}}{5}$…(4分)
②当直线l的斜率存在时,设其方程为l:y=kx+m.
联立$\left\{\begin{array}{l}y=kx+m\\{x^2}+4{y^2}=4\end{array}\right.$得:(1+4k2)x2+8kmx+4m2-4=0…(5分)
所以${x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$,…(6分)
由已知,以AB为直径的圆经过坐标原点O,则$\overrightarrow{OA}•\overrightarrow{OB}=0⇒{x_1}{x_2}+{y_1}{y_2}=0$,且${y_1}{y_2}=(k{x_1}+m)(k{x_2}+m)={k^2}{x_1}{x_2}+mk({x_1}+{x_2})+{m^2}$…(7分)
故$(1+{k^2}){x_1}{x_2}+mk({x_1}+{x_2})+{m^2}=0⇒(1+{k^2})\frac{{4{m^2}-4}}{{1+4{k^2}}}+mk\frac{-8km}{{1+4{k^2}}}+{m^2}=0$
化简得5m2=4(1+k2),…(8分)
故点O到直线AB的距离为$d=\frac{|m|}{{\sqrt{1+{k^2}}}}=\frac{{2\sqrt{5}}}{5}$
综上,点O到直线AB的距离为定值$\frac{{2\sqrt{5}}}{5}$…(9分)
法二:(若设直线方程为l:x=my+c,也要对直线斜率为0进行讨论)
设A(x1,y1),B(x2,y2),
①当直线l的斜率为0时,由椭圆对称性知x1=-x2,y1=y2,因为以AB为直径的圆经过坐标原点O,故$\overrightarrow{OA}•\overrightarrow{OB}=0⇒{x_1}{x_2}+{y_1}{y_2}=0$,即$-{x_1}^2+{y_1}^2=0$
又因为点A(x1,y1)在椭圆上,故$\frac{{{x_1}^2}}{4}+{y_1}^2=1$,解得$|{x_1}|=|{y_1}|=\frac{{2\sqrt{5}}}{5}$,
此时点O到直线AB的距离为$d=\frac{{2\sqrt{5}}}{5}$…(4分)
②当直线l的斜率不为0,或斜率不存在时,设其方程为l:x=my+c.
联立$\left\{\begin{array}{l}x=my+c\\{x^2}+4{y^2}=4\end{array}\right.$得:(m2+4)y2+2cmy+c2-4=0…(5分)
所以${y_1}+{y_2}=-\frac{2cm}{{{m^2}+4}},{y_1}{y_2}=\frac{{{c^2}-4}}{{{m^2}+4}}$,…(6分)$\begin{array}{l}故\overrightarrow{OA}•\overrightarrow{OB}=0⇒{x_1}{x_2}+{y_1}{y_2}={y_1}{y_2}+(m{y_1}+c)(m{y_2}+c)\\=(1+{m^2}){y_1}{y_2}+mc({y_1}+{y_2})+{c^2}=0⇒(1+{m^2})\frac{{{c^2}-4}}{{{m^2}+4}}-\frac{{2{c^2}{m^2}}}{{{m^2}+4}}+{c^2}=0\end{array}$…(8分)
化简得5c2=4(1+m2),故点O到直线AB的距离为$d=\frac{|c|}{{\sqrt{1+{m^2}}}}=\frac{{2\sqrt{5}}}{5}$
综上,点O到直线AB的距离为定值$\frac{{2\sqrt{5}}}{5}$…(9分)
(Ⅲ)法一:当直线OA、直线OB中有一条斜率不存在,另一条斜率为0时,易知S=1;当直线OA、直线OB斜率存在且不为0时,设直线OA的斜率为k,则直线OB的斜率为$-\frac{1}{k}$,由$\left\{\begin{array}{l}y=kx\\{x^2}+4{y^2}=4\end{array}\right.$得$\left\{\begin{array}{l}{x_1}^2=\frac{4}{{1+4{k^2}}}\\{y_1}^2=\frac{{4{k^2}}}{{1+4{k^2}}}\end{array}\right.$,同理$\left\{\begin{array}{l}{x_2}^2=\frac{{4{k^2}}}{{{k^2}+4}}\\{y_2}^2=\frac{4}{{{k^2}+4}}\end{array}\right.$…(10分)
故${S_{△AOB}}=\frac{1}{2}|OA|•OB|=\frac{1}{2}\sqrt{1+{k^2}}|{x_1}|•\sqrt{1+\frac{1}{k^2}}|{x_2}|=2\sqrt{\frac{{{{(1+{k^2})}^2}}}{{(1+4{k^2})({k^2}+4)}}}$
令1+k2=t(t>1),则$S=2\sqrt{\frac{t^2}{{4{t^2}+9t-9}}}=2\sqrt{\frac{1}{{-\frac{9}{t^2}+\frac{9}{t}+4}}}=2\sqrt{\frac{1}{{-9{{(\frac{1}{t}-\frac{1}{2})}^2}+\frac{25}{4}}}}$
故$\frac{4}{5}≤S<1$…(11分)
综上,△AOB面积S的最小值为$\frac{4}{5}$.…(12分)
法二:由(Ⅱ),①当直线l的斜率不存在时,$S=\frac{1}{2}•\frac{{4\sqrt{5}}}{5}•\frac{{2\sqrt{5}}}{5}=\frac{4}{5}$,
②当直线l的斜率存在时,5m2=4(1+k2),且点O到直线AB的距离为$d=\frac{{2\sqrt{5}}}{5}$,$|AB|=\sqrt{1+{k^2}}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{1+{k^2}}•\sqrt{{{(-\frac{8km}{{1+4{k^2}}})}^2}-\frac{{4(4{m^2}-4)}}{{1+4{k^2}}}}$=$4\sqrt{1+{k^2}}•\sqrt{\frac{{4{k^2}+1-{m^2}}}{{{{(1+4{k^2})}^2}}}}=4\sqrt{1+{k^2}}•\sqrt{\frac{{16{k^2}+1}}{{5{{(1+4{k^2})}^2}}}}$
故$S=\frac{1}{2}|AB|•d=\frac{4}{5}\sqrt{\frac{{({k^2}+1)(16{k^2}+1)}}{{{{(1+4{k^2})}^2}}}}$,…(10分)
令1+4k2=t(t≥1),则$S=\frac{2}{5}\sqrt{\frac{{4{t^2}+9t-9}}{t^2}}=\frac{2}{5}\sqrt{-\frac{9}{t^2}+\frac{9}{t}+4}=\frac{2}{5}\sqrt{-9{{(\frac{1}{t}-\frac{1}{2})}^2}+\frac{25}{4}}$,
因为$0<\frac{1}{t}≤1$,故$\frac{4}{5}≤S≤1$.…(11分)
综上,△AOB面积S的最小值为$\frac{4}{5}$.…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及分析问题解决问题的能力.考查圆锥曲线的最值问题的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
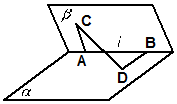 如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )
如图,在二面角α-l-β的棱l上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,BD=3,则CD=( )| A. | $\sqrt{11}$ | B. | $\sqrt{14}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
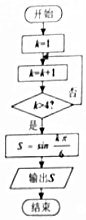
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{π}{6}$-6x) | B. | y=cos6x | C. | y=sin($\frac{2π}{3}$-$\frac{3x}{2}$) | D. | y=sin(-$\frac{π}{6}$-$\frac{3}{2}$x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {2,3,5} | C. | {1,3,4,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
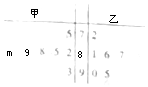 甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com