
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据对数函数指数函数的性质,分别判断三个数值的大小进行比较即可.
②利用函数与方程之间的关系,转化为两个函数的相交问题进行求解即可.
③利用对称性的性质建立方程关系,进行求解.
④根据等比数列和等差数列的性质和公式进行证明.
解答 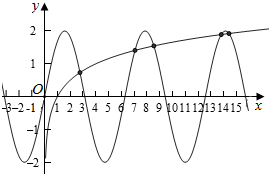 解:①∵log0.53<0,2${\;}^{\frac{1}{3}}$>1,0<($\frac{1}{3}$)0.2<1,
解:①∵log0.53<0,2${\;}^{\frac{1}{3}}$>1,0<($\frac{1}{3}$)0.2<1,
∴log0.53<($\frac{1}{3}$)0.2<2${\;}^{\frac{1}{3}}$;故①错误,
②由f(x)=log4x-2sinx=0得log4x=2sinx,
作出两个函数y=log4x和y=2sinx的图象如图:
由图象知两个函数有5个交点,即函数f(x)有5个零点;故②正确,
③设f(x)的定义域为D,?∈D,有:$f(x)+f(10-x)=ln\frac{x-4}{x-6}+\frac{x}{12}+ln\frac{6-x}{4-x}+\frac{10-x}{12}=\frac{5}{6}$,
所以,函数y=f(x)的图象关于点$(5,\frac{5}{12})$对称.
故函数f(x)=ln$\frac{x-4}{x-6}$+$\frac{x}{12}$的图象以$(5,\frac{5}{12})$为对称中心,正确;故③正确,
④∵a、b、m、n、x、y均为正数,且a≠b,且 a、m、b、x成等差数列,∴m=$\frac{a+b}{2}$.
又 a、n、b、y成等比数列,∴n=$\sqrt{ab}$,由基本不等式可得 m>n.
又 同理可得 b=$\frac{m+x}{2}$=$\sqrt{ny}$≥$\sqrt{mx}$,∴y>x.
综上,m>n,x<y,故④正确,
综上正确的是②③④,共3个,
故选:C.
点评 本题主要考查命题的真假判断,涉及函数的零点,对称性,函数值的大小比较以及等比数列和等差数列的应用,综合性较强,考查学生的运算和推理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
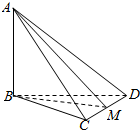
| A. | ∠ADB | B. | ∠BDC | C. | ∠AMB | D. | ∠ACB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
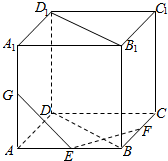 如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,
如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com