
【题目】(2017·全国Ⅱ卷)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.

(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1) 取PA的中点F,根据平几知识得四边形BCEF是平行四边形,即得CE∥BF ,再根据线面平行判定定理证结论,(2) 先根据条件建立空间直角坐标系,设立各点坐标,根据方程组各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补关系求二面角M-AB-D的余弦值.
试题解析: (1)证明 取PA的中点F,连接EF,BF,
因为E是PD的中点,所以EF∥AD,EF=![]() AD.
AD.
由∠BAD=∠ABC=90°得BC∥AD,
又BC=![]() AD,所以EF綉BC,
AD,所以EF綉BC,
四边形BCEF是平行四边形,CE∥BF,
又BF平面PAB,
CE平面PAB,
故CE∥平面PAB.
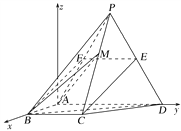
(2)解 由已知得BA⊥AD,以A为坐标原点,![]() 的方向为x轴正方向,|
的方向为x轴正方向,|![]() |为单位长,建立如图所示的空间直角坐标系A-xyz,则
|为单位长,建立如图所示的空间直角坐标系A-xyz,则
A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,![]() ),
),
![]() =(1,0,-
=(1,0,-![]() ),
),![]() =(1,0,0).
=(1,0,0).
设M(x,y,z)(0<x<1),则
![]() =(x-1,y,z),
=(x-1,y,z),![]() =(x,y-1,z-
=(x,y-1,z-![]() ).
).
因为BM与底面ABCD所成的角为45°,
而n=(0,0,1)是底面ABCD的法向量,
所以|cos〈![]() ,n〉|=sin 45°,
,n〉|=sin 45°,
![]() =
=![]() ,
,
即(x-1)2+y2-z2=0.①
又M在棱PC上,设![]() =λ
=λ![]() (0<λ≤1),则
(0<λ≤1),则
x=λ,y=1,z=![]() -
-![]() λ.②
λ.②
由①,②解得 (舍去),
(舍去),
所以M![]() ,从而
,从而![]() =
=![]() .
.
设m=(x0,y0,z0)是平面ABM的法向量,则
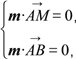 即
即![]()
所以可取m=(0,-![]() ,2).
,2).
于是cos〈m,n〉=![]() =
=![]() .
.
因此二面角M-AB-D的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
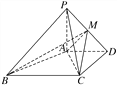
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2![]() ,BC=4
,BC=4![]() ,PA=2.
,PA=2.
(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角MACD的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,所有棱长都等于
中,所有棱长都等于![]() .
.

(1)当点![]() 是
是![]() 的中点时,
的中点时,
①求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
②求二面角![]() 的正弦值;
的正弦值;
(2)当点![]() 在线段
在线段![]() 上(包括两个端点)运动时,求直线
上(包括两个端点)运动时,求直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知四棱锥![]() 的底面
的底面![]() 为矩形,
为矩形, ![]() 底面
底面![]() ,且
,且![]() (
(![]() ),
),![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(1)当![]() 为何值时,平面
为何值时,平面![]() 平面
平面![]() ?并证明你的结论;
?并证明你的结论;
(2)当异面直线![]() 与
与![]() 所成角的正切值为2时,求三棱锥
所成角的正切值为2时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的高二女子排球比赛中,有![]() 、
、![]() 两个球队进入决赛,决赛采用7局4胜制.假设
两个球队进入决赛,决赛采用7局4胜制.假设![]() 、
、![]() 两队在每场比赛中获胜的概率都是
两队在每场比赛中获胜的概率都是![]() .并记需要比赛的场数为
.并记需要比赛的场数为![]() .
.
(Ⅰ)求![]() 大于4的概率;
大于4的概率;
(Ⅱ)求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com