Question

【题目】如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝2，BC＝4，PA＝2.

(1)求证：AB⊥PC；

(2)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．

Answer 1

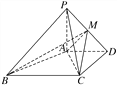
【答案】（1）见解析（2）

【解析】试题分析：（1）利用直角梯形的性质求出AB，AC的长，根据勾股定理的逆定理得出AB⊥AC，由PA⊥平面ABCD得出AB⊥PA，故AB⊥平面PAC，于是AB⊥PC；

（2）取BC的中点E，则AE⊥BC，以A为坐标原点，AE，AD，AP所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系，利用向量法表示二面角MACD根据已知条件，即可建立a的方程，从而解出a值，故存在．

试题解析：

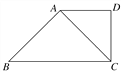
(1)证明：如图，由已知得四边形ABCD是直角梯形，

由AD＝CD＝2，BC＝4，

可得AB＝AC＝4，

所以BC2＝AB2＋AC2，

所以∠BAC＝90°，即AB⊥AC，

因为PA⊥平面ABCD，所以PA⊥AB，

又PA∩AC＝A，

所以AB⊥平面PAC，

所以AB⊥PC.

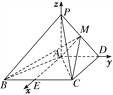
(2)存在，理由如下：取BC的中点E，则AE⊥BC，以A为坐标原点，AE，AD，AP所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系，

则A(0,0,0)，C(2，2，0)，

D(0，2，0)，P(0，0,2)，B(2，－2，0)，＝(0,2，－2)，＝(2，2，0)．

设＝t (0＜t＜1)，

则点M的坐标为(0,2t，2－2t)，

所以＝(0,2t,2－2t)．

设平面MAC的法向量是n＝(x，y，z)，

则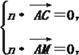即

令x＝1，得y＝－1，z＝，

则n＝.

又m＝(0,0,1)是平面ACD的一个法向量，

所以|cos〈m，n〉|＝＝＝，

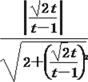解得t＝，即点M是线段PD的中点．

此时平面MAC的一个法向量n＝(1，－1，)，

又＝(－2，3，1)．

设BM与平面MAC所成的角为θ，

则sin θ＝|cos〈n，〉|＝＝.

故BM与平面MAC所成角的正弦值为.