
����Ŀ��Ϊ�о��С�Ů�������߲��죬������Ӹ߶�ij��ѡ��������Ů����![]() �ˣ����������ǵ����ߣ�����������£���λ�����ף���
�ˣ����������ǵ����ߣ�����������£���λ�����ף���
�У�![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
��![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ���ݲ������������ߵľ�Ҷͼ����λ�����ף������ֱ�����С�Ů�����ߵ�ƽ��ֵ.
���ݲ������������ߵľ�Ҷͼ����λ�����ף������ֱ�����С�Ů�����ߵ�ƽ��ֵ.
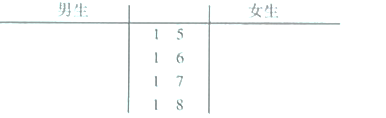
![]() ����ݲ�������õ�
����ݲ�������õ�![]() ��ѧ�����ߵ���λ����λ��
��ѧ�����ߵ���λ����λ��![]() ����λ�����ף������С�Ů���߲�����
����λ�����ף������С�Ů���߲�����![]() �͵���
�͵���![]() �����������±��У����ж��Ƿ���
�����������±��У����ж��Ƿ���![]() �İ�����Ϊ�С�Ů�����в��죿
�İ�����Ϊ�С�Ů�����в��죿

���չ�ʽ��![]()

![]() ���������ߵ���165����Ϊƫ����������165�����ҵ���175����Ϊ������������175����Ϊƫ�ߣ���������ò��������Ƶ�ʴ�����ʣ�����Ӹ���������������ѡ��2�ˣ�ǡ��1���������������ĸ���.
���������ߵ���165����Ϊƫ����������165�����ҵ���175����Ϊ������������175����Ϊƫ�ߣ���������ò��������Ƶ�ʴ�����ʣ�����Ӹ���������������ѡ��2�ˣ�ǡ��1���������������ĸ���.
���𰸡���1����������2����������3��![]()
��������
��1��������������õ������ľ�Ҷͼ����ƽ��ֵ�Ĺ�ʽ�õ�ƽ��������2�����ݿ�����ʽ�õ�����ֵ�����������жϣ���3������������������������Ϊ![]() ����������ĸ���Ϊ��
����������ĸ���Ϊ��![]() .
.
![]() ��ҶͼΪ��
��ҶͼΪ��
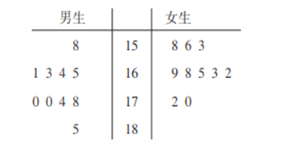
ƽ��ֵ�ǽ��������ݼӵ�һ�𣬳������ݵĸ����õ��Ľ����������һ��ʽ�����ݴ��빫ʽ���õ���ƽ�����ߣ���![]() Ů��
��![]()
![]() ������λ���ĸ���õ�
������λ���ĸ���õ�![]()
![]()
����û��![]() ������Ϊ�С�Ů�����в���.
������Ϊ�С�Ů�����в���.
��3���ɲ��������֪������������������������Ϊ![]()
���ѡ![]() ��������ǡ��һ�����������ĸ���Ϊ
��������ǡ��һ�����������ĸ���Ϊ![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
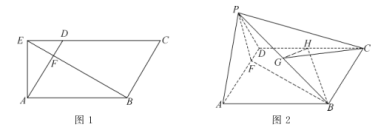
����Ŀ����ƽ���ı���![]() �У�
��![]() ��
��![]() ����
����![]() ����
����![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() .����
.����![]() ����
����![]() �ڵ�
�ڵ�![]() ����ͼ1����
����ͼ1����![]() ��
��![]() ����ʹ�õ�
����ʹ�õ�![]() �����
�����![]() ��λ�ã���ͼ2.
��λ�ã���ͼ2.
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���е㣬��ƽ��
���е㣬��ƽ��![]() ƽ��
ƽ��![]() ��������
��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
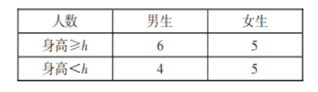
����Ŀ��Ϊ�˵��������ߵ�άȨ��ʶ���ൺ���е�ѧ�����������Ĺ㳡���������120���������ǵ�������飺��1��[20.30������2��[30��40������3��[40��50������4��[50��60������5��[60��70�����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
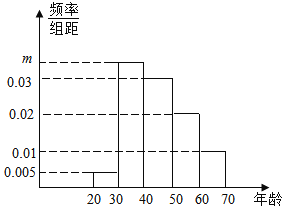
��1����Ҫ�ӱ������������ѡ1�˲ɷã��ɷ���ǡ���ڵ�2����5��ĸ��ʣ�
��2����֪��1��������������2�ˣ�ѧ��Ҫ�ӵ�1���������ȡ3���������άȨ־Ը�߷���ӣ�������������Ů�Եĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڵ�������![]() �У�
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() Ϊ
Ϊ![]() �е��ֽ��ı���
�е��ֽ��ı���![]() ��
��![]() ����,ʹƽ��
����,ʹƽ��![]() ƽ��
ƽ��![]() ���õ���ͼ����ʾ�Ķ�������ͼ���У�
���õ���ͼ����ʾ�Ķ�������ͼ���У�
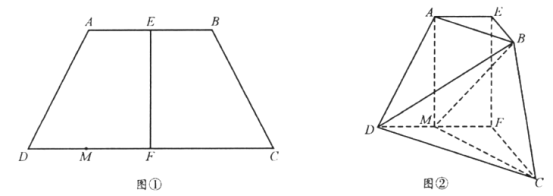
��1��֤����![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڱ߳�Ϊ3������![]() �У���֪
�У���֪![]() ����
����![]() .������
.������![]() ��ֱ��
��ֱ��![]() ����ʹ
����ʹ![]() ƽ��
ƽ��![]() ����ͼ2��
����ͼ2��![]() �ֱ���
�ֱ���![]() �ϵĵ�.
�ϵĵ�.
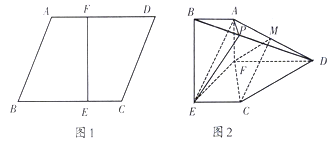
��1����֤��ͼ2�У�ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ƽ��
ƽ��![]() ��������
��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ʪ����ͼ��ʾ��A��B��C��D�ֱ����Ե�OΪ�����ڶ���������ϱ��������õ��ĸ��۲�㣬���ǵ���O�ľ����Ϊ![]() ���ʵ��PQST��һ���۹ⳤ�ȣ����У�PQ���ϵ�����һ�㵽�۲��C�ľ���ȵ��۲��D�ľ��붼��8���QS���ϵ�����һ�㵽���ĵ�O�ľ��붼��ȣ�ST���ϵ�����һ�㵽�۲��A�ľ���ȵ��۲��B�ľ��붼��8�����OΪԭ�㣬AB����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵxOy.
���ʵ��PQST��һ���۹ⳤ�ȣ����У�PQ���ϵ�����һ�㵽�۲��C�ľ���ȵ��۲��D�ľ��붼��8���QS���ϵ�����һ�㵽���ĵ�O�ľ��붼��ȣ�ST���ϵ�����һ�㵽�۲��A�ľ���ȵ��۲��B�ľ��붼��8�����OΪԭ�㣬AB����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵxOy.
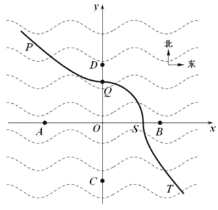
��1����۹ⳤ��PQST���ڵ����ߵķ��̣�
��2���ڹ۹ⳤ�ȵ�PQ���ϣ��轨һ����վM��ʹ�䵽�۲��A�ľ����������������÷���վM��λ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4-4������ϵ���������]
��ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
Ϊ������![]() ����������ԭ��
����������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
������![]() ����ֱ��
����ֱ��![]() ����ͨ���̼�����
����ͨ���̼�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������ֱ��![]() ������
������![]() ��������ͬ�Ľ��㣬��
��������ͬ�Ľ��㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABSCD�У��ı���ABCDΪ���Σ�AB��1����BSCΪ�߳�Ϊ2���������Σ�����BSC��BC����ʹ�ò���SAD��ֱ��ƽ��ABCD��E��F�ֱ�ΪSA��DC���е㣮
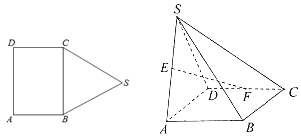
��1����֤��EF����SBC��
��2��������S��ABCD�IJ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�ΪF1��F2��������Ϊ
�����ҽ���ֱ�ΪF1��F2��������Ϊ![]() �������F2��ֱ��l����ԲC�صõ��߶�ΪMN����l��x��ʱ��|MN|��3��
�������F2��ֱ��l����ԲC�صõ��߶�ΪMN����l��x��ʱ��|MN|��3��
��1������ԲC�ı����̣�
��2����x�����Ƿ����һ��P��ʹ�õ�l�仯ʱ������PM��PN���ڵ�ֱ�߹���x��Գƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com