
已知函数f(x)=alnx+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数y=f(x)的解析式;
(2)函数g(x)=f(x)+m-ln4,若方程g(x)=0在[ ,2]上恰有两解,求实数m的取值范围.
,2]上恰有两解,求实数m的取值范围.
(1) f(x)=4lnx-x2 ;(2) 2<m≤4-2ln2.
【解析】
试题分析:(1)由切线方程知图像过 ,求导后,由题可得
,求导后,由题可得 ,分别代函数与导函数表达式,解
,分别代函数与导函数表达式,解 可得;(2)由(1)得g(x)=4lnx-x2+m-ln4,即方程m=x2-4lnx+ln4,在
可得;(2)由(1)得g(x)=4lnx-x2+m-ln4,即方程m=x2-4lnx+ln4,在 上恰有两解,令
上恰有两解,令
h(x)=x2-4lnx+ln4,由导函数得在 上递减,在(
上递减,在( ,2)上递增,可得2< h(x)≤4-2ln2,即2<m≤4-2ln2.
,2)上递增,可得2< h(x)≤4-2ln2,即2<m≤4-2ln2.
【解析】
(1)∵点P(1,f(1))在切线2x-y-3=0上,
∴2-f(1)-3=0,
∴f(1)=-1,故b=-1, 2分
又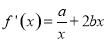 ,∴f ′(1)=a+2b=2,∴a=4,
,∴f ′(1)=a+2b=2,∴a=4,
∴f(x)=4lnx-x2. 4分
(2)g(x)=4lnx-x2+m-ln4
由g(x)=0得:m=x2-4lnx+ln4,此方程在 上恰有两解, 6分
上恰有两解, 6分
记h(x)=x2-4lnx+ln4,则
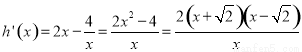 , 8分
, 8分
由h′(x)=0得:x= ∈
∈ ,
,
在 上,h′(x)<0,h(x)单调递减,
上,h′(x)<0,h(x)单调递减,
在( ,2)上,h′(x)>0,h(x)单调递增, 10分
,2)上,h′(x)>0,h(x)单调递增, 10分
又h(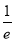 )=
)= +4+2ln2,h(
+4+2ln2,h( )=2-4ln
)=2-4ln +2ln2=2,
+2ln2=2,
h(2)=4-4ln2+2ln2=4-2ln2,
∵h(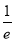 )≥h(2),∴2<m≤4-2ln2. 13分
)≥h(2),∴2<m≤4-2ln2. 13分
考点:导数的几何意义,利用导数求函数的值域.


科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:选择题
已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2= 20的两条渐近线围成的三角形的面积等于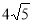 ,则抛物线的方程为
,则抛物线的方程为
A.y2=4x B.y2=8x C.x2=4y D.x2=8y
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数f(x)的导函数为f′(x),满足f(x)=2xf′(2)+x3,则f′(2)等于( ).
A.﹣8 B.﹣12 C.8 D.12
查看答案和解析>>
科目:高中数学 来源:2015届山东省潍坊市高二下学期入学考试数学试卷(解析版) 题型:选择题
.2x2-5x-3<0的一个必要不充分条件是
A.- <x<3 B.-
<x<3 B.- <x<0
<x<0
C.-3<x< D.-1<x<6
D.-1<x<6
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
在平面直角坐标系 中,已知P是函数
中,已知P是函数 (x>0)的图象上的动点,该图象在点P处的切线
(x>0)的图象上的动点,该图象在点P处的切线 交y轴于点M,过点P作
交y轴于点M,过点P作 的垂线交y轴于点N,设线段MN的中点的纵坐标为
的垂线交y轴于点N,设线段MN的中点的纵坐标为 ,则
,则 的最大值是________.
的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
 的展开式中各项系数的和为2,则该展开式中常数项为( )
的展开式中各项系数的和为2,则该展开式中常数项为( )
A.-40 B.-20 C.20 D.40
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
用二分法求方程x2=2的正实根的近似解(精确度0.001)时,如果我们选取初始区间是[1.4,1.5],则要达到精确度要求至少需要计算的次数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com