
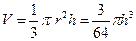 2分
2分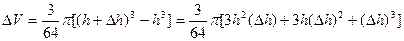 5分
5分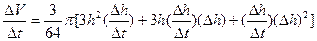 7分
7分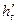 (即当
(即当 无限趋近于0时,
无限趋近于0时,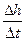 无限趋近于
无限趋近于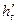 )
)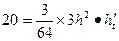 ,当h=4时,解得
,当h=4时,解得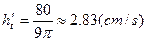 12分
12分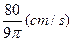 。 14分
。 14分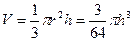 ,即
,即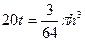 4分
4分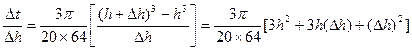 5分
5分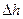 无限趋近于0时,
无限趋近于0时,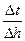 无限趋近于
无限趋近于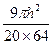 ,即
,即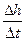 无限趋近于
无限趋近于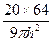 12分
12分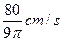 . 14分
. 14分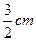 ,设水面高度增加
,设水面高度增加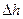 时,水的体积增加
时,水的体积增加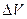 ,从而
,从而 ,(用圆柱近似增加的水体积) , 8分
,(用圆柱近似增加的水体积) , 8分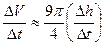 .当
.当 无限趋近于0时得
无限趋近于0时得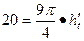 10分
10分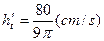 12分
12分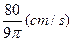 。 14分
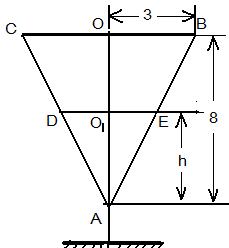
。 14分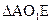 ∽
∽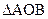 ,那么
,那么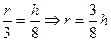 2分
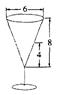
2分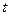 时刻时杯中水的容积为V=
时刻时杯中水的容积为V=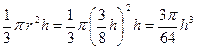 3分
3分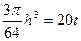 即
即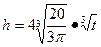 6分
6分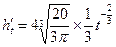 8分
8分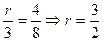 , 9分
, 9分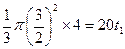
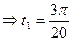 10分
10分 12分
12分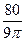 cm/s 14分
cm/s 14分

科目:高中数学 来源:不详 题型:填空题
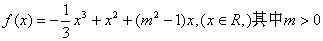
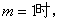 曲线
曲线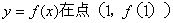 处的切线斜率
处的切线斜率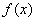 有三个互不相同的零点0,
有三个互不相同的零点0,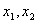 ,且
,且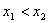 。若对任意的
。若对任意的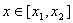 ,
,
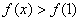 恒成立,求m的取值范围。
恒成立,求m的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
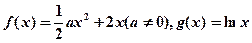 .
.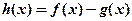 存在单调增区间,求
存在单调增区间,求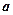 的取值范围;
的取值范围;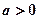 ,使得方程
,使得方程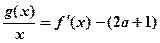 在区间
在区间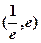 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出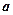 的取值范围?若不存在,请说明理由。
的取值范围?若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
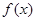 的定义域为
的定义域为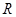 ,对任意的
,对任意的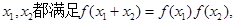
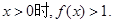
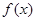 的单调性并予以证明;
的单调性并予以证明;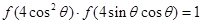 ,求
,求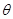 的值;
的值;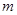 ,当
,当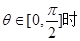 ,使不等式
,使不等式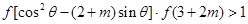 对所有的
对所有的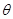 恒成立,若存在,求出
恒成立,若存在,求出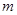 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
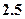 元,销售价是每束
元,销售价是每束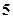 元;节后卖不出的鲜花以每束
元;节后卖不出的鲜花以每束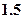
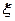 | 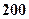 | 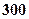 | 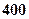 | 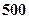 |
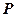 | 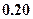 | 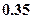 | 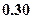 | 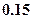 |
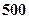 束,则期望利润是( )
束,则期望利润是( )A.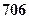 元 元 | B.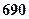 元 元 | C.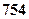 元 元 | D.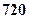 元 元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com