
分析 (I)由正弦定理化简已知等式可得2cosAsinA=sinA,结合sinA≠0,可求cosA=$\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(II)由△ABC的面积为$\frac{{\sqrt{3}}}{4}$,求出bc,利用c2+abcosC+a2=4,得出3a2+b2+c2=8,结合余弦定理求a.
解答 解:(I)由正弦定理可知,2cosA(sinBcosC+sinCcosB)=sinA,
即2cosAsinA=sinA,
因为A∈(0,π),
所以sinA≠0,
所以2cosA=1,即cosA=$\frac{1}{2}$
又A∈(0,π),
所以A=$\frac{π}{3}$;
(II)∵△ABC的面积为$\frac{{\sqrt{3}}}{4}$,
∴$\frac{1}{2}bc×\frac{\sqrt{3}}{2}$=$\frac{{\sqrt{3}}}{4}$,∴bc=1
∵c2+abcosC+a2=4,∴3a2+b2+c2=8,
∵a2=b2+c2-bc
∴4a2=7,∴a=$\frac{\sqrt{7}}{2}$.
点评 本题主要考查了正弦定理,余弦定理,两角差的正弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
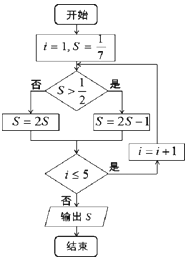
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
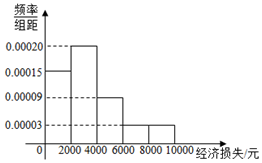 2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.| 经济损失不超过4000元 | 经济损失超过4000元 | 总计 | |
| 捐款超过500元 | 60 | ||
| 捐款不超过500元 | 10 | ||
| 总计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $\sqrt{31}$ | C. | $\sqrt{33}$ | D. | $4\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com