
【题目】已知函数f(x)=ax2+blnx在x=1处有极值 ![]() .
.
(1)求a,b的值;
(2)求函数y=f(x)的单调性.
【答案】
(1)解:∵函数f(x)=ax2+blnx,
∴ ![]() ,
,
∵f(x)在x=1处有极值 ![]() ,
,
∴ 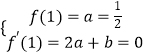 ,解得a=
,解得a= ![]() ,b=﹣1.
,b=﹣1.
(2)解:由(1)得f(x)= ![]() ,其定义域为(0,+∞),
,其定义域为(0,+∞),
且f′(x)=x﹣ ![]() =
= ![]() .
.
当x变化时,f′(x),f(x)的变化情况如下表:
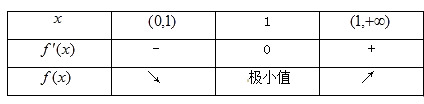
∴函数f(x)的单调减区间是(0,1),单调增区间是(1,+∞).
【解析】(1)由函数f(x)=ax2+blnx,知 ![]() ,由f(x)在x=1处有极值
,由f(x)在x=1处有极值 ![]() ,知
,知 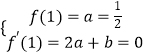 ,由此能求出a,b的值.(2)由f(x)=
,由此能求出a,b的值.(2)由f(x)= ![]() ,其定义域为(0,+∞),f′(x)=x﹣
,其定义域为(0,+∞),f′(x)=x﹣ ![]() =
= ![]() .列表讨论,能求出函数f(x)的单调区间.
.列表讨论,能求出函数f(x)的单调区间.
【考点精析】掌握利用导数研究函数的单调性和函数的极值是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】下列推理中属于归纳推理且结论正确的是( )
A.由an=2n﹣1,求出S1=12 , S2=22 , S3=32 , …,推断:数列{an}的前n项和Sn=n2
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数
C.由圆x2+y2=r2的面积S=πr2 , 推断:椭圆 ![]() =1的面积S=πab
=1的面积S=πab
D.由(1+1)2>21 , (2+1)2>22 , (3+1)2>23 , …,推断:对一切n∈N* , (n+1)2>2n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,前
,前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).
).
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
⑶ 是否存在整数对![]() (其中
(其中![]() ,
, ![]() )满足
)满足![]() ?若存在,求出所有的满足题意的整数对
?若存在,求出所有的满足题意的整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
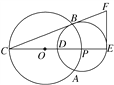
【题目】如图,圆O与圆P相交于A,B两点,圆心P在圆O上,圆O的弦BC切圆P于点B,CP及其延长线交圆P于D,E两点,过点E作EF⊥CE,交CB的延长线于点F.
(1)求证:B,P,E,F四点共圆;
(2)若CD=2,CB=2![]() ,求出由B,P,E,F四点所确定的圆的直径.
,求出由B,P,E,F四点所确定的圆的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx﹣ax(a> ![]() ),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于 .
),当x∈(﹣2,0)时,f(x)的最小值为1,则a的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市“网约车”的现行计价标准是:路程在2km以内(含2km)按起步价8元收取,超过2km后的路程按1.9元/km收取,但超过10km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆“网约车”行驶8km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=sin(x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位长度,再将图象上所有点的横坐标缩短为原来的
个单位长度,再将图象上所有点的横坐标缩短为原来的 ![]() 倍(纵坐标不变)得到函数f(x)的图象. (Ⅰ)写出函数f(x)的解析式;
倍(纵坐标不变)得到函数f(x)的图象. (Ⅰ)写出函数f(x)的解析式;
(Ⅱ)若x∈[0, ![]() ]时,关于x的方程f(x)﹣m=0有两个不等的实数根,求实数m的取值范围.
]时,关于x的方程f(x)﹣m=0有两个不等的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从A、B、C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的实数满足: ![]() ,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2015)= .
,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2015)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com