
【题目】在如图所示的几何体中,四边形![]() 是菱形,四边形
是菱形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点.
上的一点.
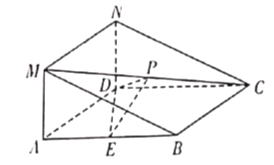
(1)求证:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)连接DB,由已知可得△ABD为等边三角形,得到DE⊥AB,则DE⊥DC,再由ADNM为矩形,得DN⊥AD,由面面垂直的性质可得DN⊥平面ABCD,得到DN⊥DE,由线面垂直的判断可得DE⊥平面DCN,进一步得到DE⊥CN;
(2)由(1)知DN⊥平面ABCD,得到DN⊥DE,DN⊥DC,又DE⊥DC,以D为坐标原点,DE、DC、DN分别为x轴、y轴、z轴建立空间直角坐标系,设![]() ,λ∈[0,1],分别求出平面PDE与平面DEC的一个法向量,由二面角P﹣DE﹣C的大小为
,λ∈[0,1],分别求出平面PDE与平面DEC的一个法向量,由二面角P﹣DE﹣C的大小为![]() 列式求得λ即可.
列式求得λ即可.
(1)连接![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,
,
![]() 为等边三角形.
为等边三角形.
又![]() 为
为![]() 的中点,
的中点,![]() .
.
又![]() ,
,![]() .
.
![]() 四边形
四边形![]() 为矩形,
为矩形,![]() .
.
又![]() 平面
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
又![]()
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 。
。
![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
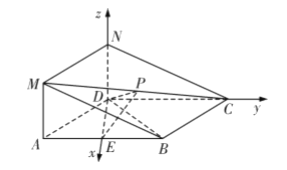
则![]() ,
,
![]() ,
,
设![]() ,
,
则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则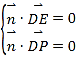 ,
,
即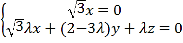 ,
,
令![]() ,则
,则![]() .
.
由图形知,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
即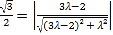 ,即
,即![]() .
.
![]() ,
,
![]() 解得
解得![]() ,
,![]() 的值为
的值为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 命题“若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
B. 命题“存在![]() ”的否定是:“任意
”的否定是:“任意![]() ”
”
C. 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题
D. 已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下面四个命题,其中正确命题的序号是( )
①“直线![]() 、
、![]() 不相交”是“直线
不相交”是“直线![]() 、
、![]() 为异面直线”的充分而不必要条件;②“直线
为异面直线”的充分而不必要条件;②“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;③“直线
”;③“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;④“直线
所在的平面”;④“直线![]() 平面
平面![]() ”的必要而不充分条件是“直线
”的必要而不充分条件是“直线![]() 平行于
平行于![]() 内的一条直线.”
内的一条直线.”
A.①③B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
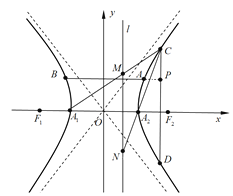
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫、精准脱贫”的号召,某贫困县在精准推进上下实功,在在精准落实上见实效现从全县扶贫对象中随机抽取![]() 人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分
人对扶贫工作的满意度进行调查,以茎叶图中记录了他们对扶贫工作满意度的分数(满分![]() 分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于
分)如图所示,已知图中的平均数与中位数相同.现将满意度分为“基本满意”(分数低于平均分)、“满意”(分数不低于平均分且低于![]() 分)和“很满意”(分数不低于
分)和“很满意”(分数不低于![]() 分)三个级别.
分)三个级别.

(1)求茎叶图中数据的平均数和![]() 的值;
的值;
(2)从“满意”和“很满意”的人中随机抽取![]() 人,求至少有
人,求至少有![]() 人是“很满意”的概率.
人是“很满意”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com