
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )
《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )| A. | 输出的数组都是勾股数 | B. | 任意正整数都是勾股数组中的一个 | ||
| C. | 相异两正整数都可以构造出勾股数 | D. | 输出的结果中一定有a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
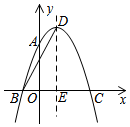 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2>b2 | C. | a+b≥2$\sqrt{ab}$ | D. | a2+b2>2ab |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com