练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．《周髀算经》记载了勾股定理的公式与证明，勾股定理相传由商高（商代）发现，故又有称之为商高定理，满足等式a2+b2=c2的正整数组（a，b，c）叫勾股数，如（3，4，5）就是勾股数，执行如图所示的程序框图，如果输入的数是互相不相等的正整数，则下面四个结论正确的是（　　）
    A．输出的数组都是勾股数B．任意正整数都是勾股数组中的一个
    C．相异两正整数都可以构造出勾股数D．输出的结果中一定有a＜b＜c

    分析 由程序框图可知，正整数组（a，b，c）满足等式a2+b2=c2，即可得出结论．

    解答 解：由程序框图可知，正整数组（a，b，c）满足等式a2+b2=c2，从而相异两正整数都可以构造出勾股数．
    故选C．

    点评 本题考查程序框图，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．某企业生产的新产品必须先靠广告打开销路，该产品广告效应y（单位：元）是产品的销售额与广告费x（单位：元）之间的差，如果销售额与广告费x的算术平方根成正比，根据对市场的抽样调查，每付出100元的广告费，所得销售额是1000元．
    （Ⅰ）求出广告效应y与广告费x之间的函数关系式；
    （Ⅱ）该企业投入多少广告费才能获得最大的广告效应？是不是广告费投入越多越好？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知直线l与坐标轴不垂直且横、纵截距相等，圆C：（x+1）2+（y-2）2=r2，若直线l和圆C相切，且满足条件的直线l恰好有三条，则圆的半径r的取值集合为（　　）
    A．$\left\{{1，\sqrt{5}}\right\}$B．$\left\{{\sqrt{5}，\frac{{\sqrt{2}}}{2}}\right\}$C．$\left\{{1，\sqrt{5}，\frac{{\sqrt{2}}}{2}}\right\}$D．$\left\{{1，2，\sqrt{5}，\frac{{\sqrt{2}}}{2}}\right\}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，倾斜角为α（α≠$\frac{π}{2}$）的直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$（t为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程是ρcos2θ-4sinθ=0．
    （Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；
    （Ⅱ）已知点P（1，0），若点M的极坐标为（1，$\frac{π}{2}$），直线l经过点M且与曲线C相交于A，B两点，设线段AB的中点为Q，求|PQ|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知AB是直角△ABC的斜边，$\overrightarrow{CA}=（2，4）$，$\overrightarrow{CB}=（-6，x）$，则x的值是（　　）
    A．3B．-12C．12D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知函数$f（x）=\frac{n}{x}（n∈{N^*}）$，过点P（n，f（n））与y=f（x）的图象相切的直线l交x轴于A（xn，0），交y轴于B（0，yn），则数列$\{\frac{1}{{{x_n}（{x_n}+{y_n}）}}\}$的前n项和为$\frac{n}{4n+4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

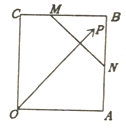    12．如图，已知正方形OABC边长为3，点M，N分别为线段BC，AB上一点，且2BM=MC，AN=NB，P为△BNM内一点（含边界），设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$（λ，μ为实数），则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．不等式3x-5＞5x+3的解集{x|x＜-4}；不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8＞4x-1}\end{array}\right.$的整数解是1和2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．从装有2个红球和 2个白球的口袋内任取2个，则互斥但不对立的两个事件是（　　）
    A．至少一个白球与都是白球B．至少一个白球与至少一个红球
    C．恰有一个白球与 恰有2个白球D．至少一个白球与都是红球

    查看答案和解析>>

    同步练习册答案