
���� ������ȥ�����õ�ֱ��l����ͨ���̡����ü�������ֱ������Ļ����������������C��ֱ�����귽�̣�
���������⣬ֱ��l�ķ���Ϊx+y-1=0����x2=4y�����ɵ�x2+4x-4=0�����Q�����꣬������|PQ|��ֵ��
��� �⣺������б��Ϊ��������$\frac{��}{2}$����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+tcos��}\\{y=tsin��}\end{array}\right.$��tΪ����������ͨ����Ϊy=tan����x-1����
����C�ļ����귽���Ǧ�cos2��-4sin��=0��ֱ�����귽��x2=4y��
���������⣬ֱ��l�ķ���Ϊx+y-1=0����x2=4y�����ɵ�x2+4x-4=0��
���߶�AB���е�ĺ�����Ϊ-2��������Ϊ3����Q��-2��3����
��|PQ|=$\sqrt{��1+2��^{2}+��0-3��^{2}}$=3$\sqrt{2}$��
���� ���⿼��������̡������귽�̡�ֱ�����귽�̵Ļ���������ֱ���������ߵ�λ�ù�ϵ�������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ϕ | B�� | {1��2} | C�� | {-1��1��2} | D�� | {2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �������㾭�������˹��ɶ����Ĺ�ʽ��֤�������ɶ����ഫ���̸ߣ��̴������֣������г�֮Ϊ�̸߶����������ʽa2+b2=c2���������飨a��b��c���й��������磨3��4��5�����ǹ�������ִ����ͼ��ʾ�ij����ͼ�������������ǻ����ȵ����������������ĸ�������ȷ���ǣ�������
�������㾭�������˹��ɶ����Ĺ�ʽ��֤�������ɶ����ഫ���̸ߣ��̴������֣������г�֮Ϊ�̸߶����������ʽa2+b2=c2���������飨a��b��c���й��������磨3��4��5�����ǹ�������ִ����ͼ��ʾ�ij����ͼ�������������ǻ����ȵ����������������ĸ�������ȷ���ǣ�������| A�� | ��������鶼�ǹ����� | B�� | �������������ǹ��������е�һ�� | ||
| C�� | �����������������Թ���������� | D�� | ����Ľ����һ����a��b��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
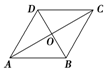
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com