
分析 (1)由题意和奇函数的性质得f(-1)=-f(1),代入解析式列出方程求出a,可求出f(x)并判断出f(x)的单调性,由条件和单调性列出关于m的不等式,求出m的取值范围;
(2)根据函数的单调性和条件,分两种情况列出不等式组,求出k的值.
解答 解:(1)∵函数$f(x)=\frac{{{x^2}+ax+4}}{x}$为奇函数,
∴f(-1)=-f(1),则-(1-a+4)=-(1+a+4),解得a=0,
即$f(x)=\frac{{x}^{2}+4}{x}$=$x+\frac{4}{x}$,
∴f(x)在(0,2)上是减函数,在(2,+∞)上是增函数,
∵函数f(x)在区间$[{\frac{m}{2},m}]({m>0})$上为单调函数,
∴m≤2或$\frac{m}{2}≥2$,则0<m≤2或m≥4,
∴m的取值范围是(0,2]∪[4,+∞);
(2)由(1)知,
f(x)在(0,2)上是减函数,在(2,+∞)上是增函数,
∵f(x)在区间[1,k]上的最小值为3k,
∴$\left\{\begin{array}{l}{1<k≤2}\\{f(k)=k+\frac{4}{k}=3k}\end{array}\right.$或$\left\{\begin{array}{l}{k≥2}\\{f(2)=2+\frac{4}{2}=3k}\end{array}\right.$,
解得k=$\sqrt{2}$或k=$\frac{4}{3}$(舍去),
即k的值是$\sqrt{2}$.
点评 本题考查函数奇偶性的性质,以及对号函数的单调性的应用,考查方程思想,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设三角形的内角三个内角中没有一个是钝角 | |
| B. | 假设三角形的内角三个内角中至少有一个是钝角 | |
| C. | 假设三角形的内角三个内角中至多有两个是钝角 | |
| D. | 假设三角形的内角三个内角中至少有两个是钝角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
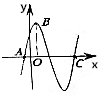 如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )
如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )| A. | (0,$\frac{5π}{8}$) | B. | ($\frac{5π}{8}$,$\frac{5π}{3}$) | C. | ($\frac{5π}{3}$,2π) | D. | ($\frac{5π}{3}$,$\frac{5π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 010 | C. | 4 018 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com