
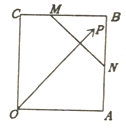
 如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$.
如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$. 分析 如图,以OA为x轴,以OC为y轴,建立直角坐标系,表示各点的坐标,根据向量的坐标运算得到λ$-\frac{1}{3}μ$=$\frac{x}{3}$-$\frac{y}{9}$=$\frac{1}{9}$(3x-y),构造目标函数,利用可行域即可求出最值.
解答 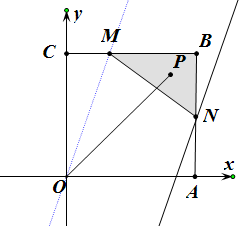 解:如图,以OA为x轴,以OC为y轴,建立直角坐标系,
解:如图,以OA为x轴,以OC为y轴,建立直角坐标系,
则O(0,0),A(3,0),C(0.3),B(3,3),
∵2BM=MC,AN=NB,
∴M(1,3),N(3,$\frac{3}{2}$),
设P(x,y),
∵$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),
∴$\overrightarrow{OP}$=λ(3,0)+μ(0,3)=(3λ,3μ),
∴$\left\{\begin{array}{l}{x=3λ}\\{y=3μ}\end{array}\right.$,即$\left\{\begin{array}{l}{λ=\frac{x}{3}}\\{μ=\frac{y}{3}}\end{array}\right.$,
∴λ$-\frac{1}{3}μ$=$\frac{x}{3}$-$\frac{y}{9}$=$\frac{1}{9}$(3x-y),
令z=3x-y,即y=3x-z,
由M(1,3),N(3,$\frac{3}{2}$),得到直线MN的方程为3x+4x-15=0,
则x,y满足的区域为$\left\{\begin{array}{l}{1≤x≤3}\\{\frac{3}{2}≤y≤3}\\{3x+4y-15≥0}\end{array}\right.$,如图所示,
当目标函数z=3x-y,过点N(3,$\frac{3}{2}$)时,Z最大,
则zmax=3×3-$\frac{3}{2}$=9-$\frac{3}{2}$=$\frac{15}{2}$,
∴(λ$-\frac{1}{3}μ$)max=$\frac{1}{9}$×$\frac{15}{2}$=$\frac{5}{6}$
故答案为:$\frac{5}{6}$
点评 本题考查了向量的坐标运算和和线性规划的问题,关键是构造目标函数,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )
《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )| A. | 输出的数组都是勾股数 | B. | 任意正整数都是勾股数组中的一个 | ||
| C. | 相异两正整数都可以构造出勾股数 | D. | 输出的结果中一定有a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
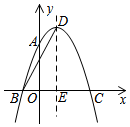 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com