
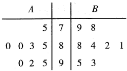
 ��A��B��C��D��E��λͬѧ�μ�Ӣ����ᄎ����ѵ���ֱַ��A��B��������ѵ�ڼ�μӵ����ɴ�Ԥ���ɼ��������ȡ8�εõ����������ݣ����������ݵ�������Ҷͼ��ͼ��ʾ��
��A��B��C��D��E��λͬѧ�μ�Ӣ����ᄎ����ѵ���ֱַ��A��B��������ѵ�ڼ�μӵ����ɴ�Ԥ���ɼ��������ȡ8�εõ����������ݣ����������ݵ�������Ҷͼ��ͼ��ʾ������ ��1�������������������������˵�ƽ�����ͷ����ƽ�����ͷ�����бȽϣ��õ������˵�ƽ������ȣ�Ȼ����ݷ����Ƿ�ӳ�ȶ��̶ȵģ��ȽϷ��ԽС˵��Խ�ȶ���
��2����5�������������˵Ŀ��������10�֣�ÿ�ֽ�����ֵĿ�������ͬ���ǡ�A��B���˶�û�вμӾ�����Ϊ�¼�M����M�����Ľ����3�֣��ɵȿ����¼��ĸ��ʿ���
��� �⣺��1����B�μӱȽϺ��ʣ��������£�
$\overline{{X}_{A}}$=$\frac{1}{8}$��75+80+80+83+85+90+92+95��=85��
$\overline{{X}_{B}}$=$\frac{1}{8}$��78+79+80+83+85+90+92+95��=85��
S2A=$\frac{1}{8}$[��75-85��2+��80-85��2+��80-85��2+��83-85��2+��85-85��2+��90-85��2+��92-85��2+��95-85��2]=41��
S2B=$\frac{1}{8}$[��78-85��2+��79-85��2+��80-85��2+��83-85��2+��85-85��2+��90-85��2+��92-85��2+��95-85��2]=35.5
��$\overline{{X}_{A}}$=$\overline{{X}_{B}}$��S2B��S2A��
��B�ijɼ����ȶ�����B�μӱȽϺ��ʣ�
��2���Ӳμ���ѵ��5λͬѧ�������������У�
��A��B������A��C������A��D������A��E������B��C����
��B��D������B��E������C��D������C��E������D��E����10�������
A��B���˶����μӣ�C��D������C��E������D��E����3�֣�
����A��B���˶�û�вμӾ����ĸ���P=$\frac{3}{10}$
���� �����������ݣ�ͨ��Ҫ������������ݵķ����ƽ������������������������ʾ�ֱ��ʾ�������ݵ���������ƽ��ˮƽ���ȶ��̶ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ�������� | B�� | �۽������� | C�� | ���������� | D�� | �ȱ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | ��-1��0�� | C�� | ��-�ޣ�-1�� | D�� | ��-�ޣ�-1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��EΪ����ABCD����ƽ����һ�㣬AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE��
��ͼ��EΪ����ABCD����ƽ����һ�㣬AD��ƽ��ABE��AE=EB=BC=2��FΪCE�ϵĵ㣬��BF��ƽ��ACE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | yƽ������2����λ | B�� | yƽ������3����λ | ||
| C�� | yƽ������2����λ | D�� | yƽ������3����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com